english

1) Baumethoden

Über handwerkliche Techniken beim Didgeridoo-Bau kann man sich in der Szene (soweit zugänglich) umfassend informieren. Da ich mit dem Material Holz arbeiten wollte, standen für mich die Sandwichmethode ( von Eddy Halat, Stefan Thiel, Jan-Ole Haber, Kay Reimer, u.a. praktiziert) oder die Bohrmethode (von Walter Strasser, Johannes Schildkamp, u.a. in verschiedenen Variationen praktiziert) zur Wahl. Leider habe ich bis jetzt noch nichts über „dressierte Termiten“ in Mitteleuropa gehört.

So interessant auch die von einigen Baukünstlern praktizierte Bohrmethode ist, entschied ich mich für die einfachere Sandwichmethode, da mit dieser wesentlich komplexere Innenformen praktisch realisierbar sind. Während Recherchen zu diesen Methoden lernte ich neben anderen interessanten Didgeridoo-Bau-Künstlern den Test-A-Doo Experimentator Kay Reimer kennen, dessen akustische Experimente mich sehr beeindruckten. Nach seiner Web-Anleitung baute ich dann auch mein erstes eigenes Holz-Didgeridoo.

Birkenholz Didgeridoo Grundton F# erster Overblow A2 

An diesen einfachen, idealisierten Formen war ich weniger interessiert, weil die damit erzeugbaren Klangcharakteristiken sehr beschränkt sind und bei Abweichungen von diesen Bauformen die berechneten Frequenzen nicht mehr stimmen.

Es mußte eine andere Methode her! 

Bei der Transmission-Line-Modellierung (Tafel 3) wird ein Didgeridoo mathematisch in eine endliche Anzahl zylindrischer und konischer Teilstücke zerlegt. Für die so modellierten beliebigen Didgeridoo-Innenformen kann dann die akustische Kettenmatrix im Bereich der komplexen Zahlen unter Berücksichtigung von Innenwandrauhigkeiten gelöst werden. Man erhält sogenannte Eingangsimpedanzspektren, aus denen die Frequenzen und der Gegendruck des Grundtones und der Overblowreihe ablesbar sind.

Durch die trickreiche Kopplung dieser Impedanzspektren mit den jeweils mitschwingenden simulierten Obertonspektren beim Spielen des Grundtones oder Overblows erhält man zusätzlich eine Näherung der Klangspektren für den Grundton und den ersten Overblow. Diese simulierten Klangspektren stimmen relativ gut mit den praktisch analysierbaren FFT-Spektrogrammen beim Spielen der jeweiligen Instrumente überein.

Um jederzeit eine Zuordnung zu den musikalischen Tonbezeichnungen herstellen zu können, sind in dieser Tabelle den Tönen die jeweiligen Frequenzen zugeordnet.

Tonfrequenzen in Hz (temperierte Stimmung)

Der grau unterlegte Bereich zeigt die Grundtonfrequenzen bei denen die meisten Didgeridoos schwingen.

Das folgende Beispiel zeigt die Klang-Simulation eines real ausgemessenen Didgeridoos von Walter Strasser und die dazugehörige praktische Analyse des FFT-Spektrogramms mit einem FFT-Analyse-Programm.

Didgeridoo von Walter Strasser: schwarz: Simulation der Overblowreihe;
 grau: Simulation des Klangspektrums beim Spielen des Grundtones;
 (L=135 cm, dMund=30 mm, dBell=110 mm; Grundton E1, erster Overblow A3+ ) gekennzeichnet durch „singenden“ 3.Oberton bei E3 lauter als der Grundton E1

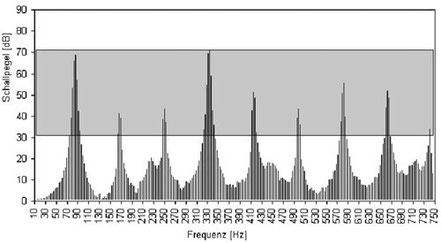
Praktische des Analyse des FFT-Spektrums beim Spielen des Grundtones:

Der dargestellte Schallpegel ist eine relative logarithmische Größe, die den Unterschied zwischen Schalldrücken beschreibt. Für die Interpretation dieser Spektren ist aber das subjektive Lautstärkeempfinden von gleichzeitig erklingenden Frequenzen wichtig. Ohne dieses Thema weiter zu vertiefen, kann davon ausgegangen werden, dass vom höchsten Peak (also der lautesten Frequenz) nur noch die Frequenzen den Klangcharakter signifikant beeinflussen, die ca. bis 40 dB unter dem höchsten Peak liegen. Alle leiseren Frequenzen werden durch die lauteren überdeckt. D.h., für jedes FFT-Spektrum existiert ein Schallpegelbereich (grauer Kasten), der signifikant die Klangcharakteristik bestimmt.

1) Baumethoden

In the didge scene there are opportunities to thoroughly inform yourself about the crafting skills needed to make the instrument. Because I wanted to work with wood, I had the choice between the sandwich method (used by Eddy Halat, Stefan Thiel, Jan-Ole Haber, Kay Reimer, and others) and the drilling method (used by Walter Strasser, Johannes Schildkamp and others in several variations). Unfortunately I’ve yet to hear of “trained termites” in central Europe.

Interesting though the drilling method used by a few craft artists is, I opted for the simpler sandwich method because it allows considerably more complex internal forms to be realized. While I was researching the methods I got to know some interesting didgeridoo makers, including the Test-A-Doo experimenter, Kay Reimer, whose acoustic experiments impressed me very much. I followed his web instructions to make my own first wooden didgeridoo.

Birch wood didgeridoo fundamental tone F# first overblow A2 

I was not very interested in these simple, idealized forms, because the sound characteristics that can be generated in this way are very limited and are not correct in the case of deviations from these idealized forms.

I had to find another method!

With this transmission line modelling, a didgeridoo is mathematically split into a finite number of cylindrical and conical pieces. The acoustic chain matrix in the complex numbers sector can be resolved for thus modelled inner cavities of didgeridoos, taking into account the uneven inside walls. In this way one obtains the so-called input impedance spectra, from which the resonant frequencies of the air column and the back-pressure of the drone (fundamental tone) and toots (series of overblows) can be read.

By tricky coupling the impedance spectra with the respective simulated harmonic spectra when playing the drone or toots, one obtains additionally an approximation of the sound spectra for the drone and the first toot. These simulated sound spectra match relatively well with the practically analysable FFT (Fast Fourier Transformation) spectrograms when the individual instruments are played.

In order to be able to achieve an allocation to the musical notes designations at any time, the respective frequencies are assigned to the tones in this table:

Audio frequencies in Hz

The range marked in grey shows the fundamental tone frequencies in which most didgeridoos resonate.

The following example shows the sound simulation of actual measurements of one of Walter Strasser’s didgeridoos and the accompanying practical analysis of the FFT spectrogram with an FFT analysis program.

Walter Strasser’s didgeridoo:
black: simulation of the toot sequences (drone and overblows);
grey: Simulation of the sound spectrum when the drone is played;
(L=135 cm, dMouth=30 mm, dBell=110 mm; Drone E1, first toot A3+ ) characterized by “singing” fourth harmonic at E3 louder than the drone E1

Practical analysis of the FFT spectrum when playing the drone:
The sound level depicted is a relative logarithmic value expressing the difference between acoustic pressures. However, to interpret these spectra the subjective perception of volume of the concurrently sounding frequencies is important. Without going further into this topic, it can be assumed that from the highest peak (i.e. the loudest frequency) only those frequencies still significantly influence the sound character which are up to about 40 dB below the highest peak. All quieter frequencies are overlaid by the louder ones. That means that for every FFT spectrum there exists a sound level section (gray box), that significantly determines the sound characteristic.