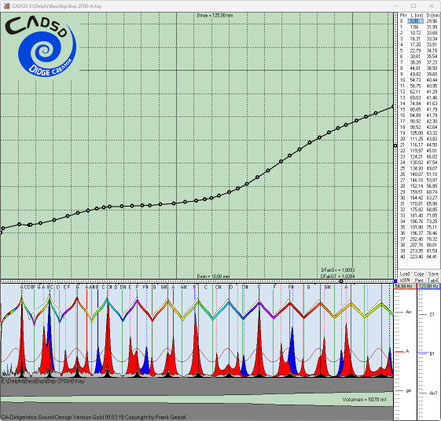
Typischer CADSD Prozess
Ich erhalte immer wieder Anfragen, warum ich die von mir entwickelten und verwendeten Softwaretools nicht für die allgemeine Verwendung zur Verfügung stelle. Da ich forschender
Wissenschaftler bin, war es ehrlich gesagt nie ein Primärziel eine derartig komplexes Thema in einer Software anzubieten. Ich hatte das früher mal mit Simulations- und Optimierungssoftware
für komplexe dynamische Systeme mit offener frei definierbarer mathematischer Modellschnittstelle gemacht und gemerkt, dass derartige Software schwer beherrschbar ist, da über 98% der damaligen
„Kundenprobleme“ durch mangelndes Verständnis der jeweiligen mathematisch wissenschaftlichen Zusammenhänge selbst verursacht wurden. D.h., der Befähigungsaufwand für die erfolgreiche Verwendung
derartiger Software und der dafür erforderlichen Pflege ist sehr hoch. Mit der „Directed Evolution“ verhält es sich ähnlich. Und als forschender Wissenschaftler mit begrenzter Zeit möchte ich
diese für die weitere Erkenntnisgewinnung nutzen und nicht für die Betreuung der sich ständig ändernden Software für optionale Kunden „vergeuden“.
Die entwickelten Tools sind nur in einer lizenzierten Programmierumgebung mit zusätzlichen Libraries verwendbar und bringen nur einem ausgesprochenen Spezialisten auf diesem Gebiet erfolgreiche
Ergebnisse und erfordern eine wissensbasierte von außen iterativ gelenkte Lösungsfindung. Zumindest wenn es um akustische Spezialitäten geht.
Inspiriert durch meine Arbeiten und die publizierten Ansätze im Buch „Das Didgeridoo Phänomen“ haben inzwischen einige Interessenten meine ersten Ideen in Open Source nachprogrammiert. Z.B.,
DIDGMO oder DIDJIMP. Diese Versionen sind für einfache Spezifikationen verwendbar, aber beinhalten nicht das gesamte wissenschaftliche Know How und auch keine Directed-Evolution.
Um interessierten Menschen einen Eindruck zu vermitteln, wie ein typischer CADSD Prozess verläuft, möchte ich im Folgenden diesen erläutern:
1. Gewünschte Spezifikation:
Am Anfang steht die Spezifikation des gewünschten Instruments. Dieser Punkt scheint erst einmal einfach. Aber jeder, der versucht seine Vorstellungen vom Klang und der Spielbarkeit eines Instrumentes zu definieren, wird merken, dass es nicht so einfach ist, die selbst gewünschten oft nur unscharf zu beschreibenden Eigenschaften in harte physikalische Ziele mathematisch zu formulieren. Deshalb erfordert es in der Regel eine gute anfängliche Konversation, um auf Basis der daraus erhaltenen Antworten iterativ die physikalischen Ziele für das Instrumentendesign zu extrahieren.
Beispiele für Spezifikationen:
- Grundton
- Folge der Toots
- Anspielbarkeit bestimmter Toots
- für Könner anspielbare PseudoToots
- anspielbare offene Flötentöne
- Gegendruck
- betonte prominente Obertöne (Singtöne)
- gewünschte Oberton Wobbel Muster (Harmonic Wobble Pattern)
- Stimmenübertragungsverhalten
- Verstärkung bestimmter Mischtöne (Heterodynes) aus Grundton und Stimme
- Ausschwingverhalten des Instruments
Wie im Kapitel „Akustische Fusionen“ beschrieben, werden oft in Spezifikationen Charakteristiken bzw. Effekte gewünscht, die sich
physikalisch ausschließen und dadurch nicht realisierbar sind. Prinzipiell gilt auch die Aussage:
Je mehr Effekte parallel in einem Instrument gekoppelt werden sollen, desto größer wird die spielerische und klangliche Flexibilität des Instrumentes und desto geringer ist die typische
Ausprägung jedes einzelnen Effektes.
2. Physikalische Möglichkeiten:
Die vorgegebene Geometrie der Innenform des Instrumentes, also der sich ergebenden schwingenden Luftsäule, bestimmt die Klang- und Spieleigenschaften. Durch den Querschnittsverlauf (Geometrie)
der Innenform ist prinzipiell nur die Lage und die Höhe der sich ergebenen intrinsischen Impedanzpeaks in physikalisch möglichen Grenzen beeinflussbar. Und nur mit der Lage und Höhe der zur
Verfügung stehenden Impedanzpeaks sind alle die unter Spezifikationen beschriebenen Eigenschaften beeinflussbar.
So stehen z.B. bei einem leicht konischen Instrument der Länge 125 cm ca. 7-8 Impedanzpeaks im Bereich von 0 - 1000 Hz zur Verfügung. Bei Verdopplung der Länge auf 250 cm verdoppelt sich die
Anzahl der Impedanzpeaks auf 14-16.
Für die Realisierung einer spezifizierten Eigenschaft wird je nach Eigenschaft die Definition der Lage und Höhe von ca. 1-3 Impedanzpeaks benötigt. Daraus wird klar, dass in der Regel nur die parallele Realisierung einer begrenzten Kombination aus gewünschten spezifizierten Eigenschaften möglich ist. D.h., bei zu viel spezifizierten Wunscheigenschaften wird es erforderlich sein, den besten Kompromiss aus der möglichen Kombination von Eigenschaften zu finden, der die Spezifikation erfüllt.
Folgende Regeln sind zu beachten:
- Der Grundton liegt in der Regel ca. 2-3% über der Frequenz des ersten Eingangs-Impedanzpeaks. Der genaue Wert ist u.a. abhängig von der Gesamtgeometrie des Instrumentes und dem individuellen Spielansatz und kann von geübten Spielern beeinflusst werden.
- Die Folge der anspielbaren Toots wird durch die Lage der weiteren Eingangs-Impedanzpeaks bestimmt.
- Die Anspielbarkeit der Toots wird in der Regel besser, je höher der jeweilige Impedanzpeak ist. Sie kann weiter verbessert werden, je mehr Obertöne (Harmonische) des jeweiligen Toots durch weitere Impedanzpeaks unterlegt sind. Dadurch erhöht sich die Harmonizität des betreffenden Toots und die dafür verwendeten Impedanzpeaks stehen nicht mehr zur Unterstützung anderer Effekte zur Verfügung.
- Soll ein durch Könner anspielbarer PseudoToot innerhalb der ersten beiden Oktaven des Grundtones realisiert werden, so müssen ca. die nächsten 1-4 Obertöne (Harmonischen) der gewünschten PseudoToot-Frequenz durch die darauffolgenden Impedanzpeaks unterlegt werden. Damit ist dann aber auch deren Verwendung für andere Effekte eingeschränkt.
- Um anspielbare offene Flötentöne zu definieren, muss die Innenform des Instrumentes so gewählt werden, dass die zwischen den Impedanzpeaks liegenden Frequenzen der Impedanzminima (negative Peaks) unter den jeweils gewünschten Flötentönen liegen. Dies ist möglich, aber schränkt dadurch auch die Möglichkeiten der Platzierung der Impedanzpeaks ein.
- Der spürbare Gegendruck eines Instrumentes wächst mit dem akustischen Scheinwiderstand am Mundstück. Dieser wird durch die Höhe des jeweilig angespielten Impedanzpeaks des Tons und seiner Harmonizität bestimmt. Um eine hohe Harmonizität zu erreichen, müssen möglichst viele der jeweiligen Obertöne (Harmonischen) des gespielten Tons durch die darauffolgenden Impedanzpeaks unterlegt werden. Auch das schränkt wieder die Verwendung dieser Impedanzpeaks für andere Effekte ein.
- Um bestimmte Obertöne prominenter als Singtöne hörbar zu machen, ist es erforderlich, deren Ausgangsimpedanz am Bellend niedrig zu halten (dadurch wird die relative Schallschnelle am Bellend maximiert), um die Übertragung deren Schallenergie an die Umgebung zu unterstützen. In der Regel liegen die Ausgangs-Impedanzpeaks am Bellend oft deckungsgleich zusammen mit denen von uns verwendeten Impedanzpeaks, die eigentlich die Eingangs-Impedanzpeaks am Mundstück sind und etwas über die Anspielbarkeit der betreffenden Töne aussagen. Werden diese relativ niedrig gehalten, verbessert sich in der Regel die Hörbarkeit der betreffenden Obertöne. Nachteil ist, dass sich dadurch deren Anspielbarkeit als Toots verschlechtert. Das stellt aber in der Regel kein Problem dar, da oft die gewünschten gut hörbaren Obertöne in einem so hohen Frequenzbereich liegen, wo anspielbare Toots nicht gewünscht sind.
- Prinzipiell gelten die gleichen Zusammenhänge, wie sie für gut hörbare Singtöne beschrieben sind auch für die gut wahrnehmbaren Oberton-Wobbels (Harmonic Wobbles). Nur mit dem Unterschied, dass mindestens zwei gewünschte Obertöne durch zwei symmetrisch um 2-3% nach außen verlagerte kleinere Impedanzpeaks unterlegt werden.
- Das vom Grundton und von den unteren Toots unabhängige Übertragungsverhalten von Stimmeffekten (z.B. Nachahmen von Tierstimmen) kann verbessert werden, wenn der Verlauf der Impedanzpeaks im Bereich von ca. 800 - 2000 Hz minimiert wird. Damit wird quasi die Impedanz-Formante des Vokaltraktes am wenigsten gehemmt und die Stimme kann sich besser entfalten. Meist sind dazu großvolumigere Instrumente besser geeignet.
- Um Mischtöne (Heterodynes) aus Stimmton einer Quinte über dem Grundton und diesem Grundton zu unterstützen, sind jegliche Frequenzen genau aus dem Mittelwert der jeweils beiden benachbarten Obertonfrequenzen ab der 2.Oktave zum Grundton mit einem Impedanzpeak zu unterlegen. Also an den Frequenz-Verhältnissen 5/2, 7/2, 9/2, 11/2, 13/2, 15/2, 17/2, … (je kleiner die Verhältnisse, um so wirksamer);
- Das Ausschwingverhalten eines Instrumentes wird dann länger, wenn die Dämpfung der schwingenden Luftsäule minimiert wird. Das ist in der Regel möglich durch großvolumigere Instrumente und einer mikroskopisch glatten Innenoberfläche. Weiterhin ist das Ausschwingverhalten meist auch bei Instrumenten mit relativ glatten Querschnittsverlauf ohne viele steile Einengungen verlängert. Bei zu vielen Einengungen kann sich das Schwingverhalten soweit verschlechtern, dass derartige Instrumente nur noch schwer oder gar nicht spielbar sind.
3. Directed-Evolution Process:
Mit der CADSD-Methode ist es im Prinzip nur möglich, beliebige Innenformen vorzugeben und die damit erzeugbaren Klang- und Impedanz-Spekteren zu berechnen. Leider ist es mathematisch nicht
möglich, ein Ziel-Spektrum vorab einzustellen und automatisch Vorschläge für entsprechende Innenformen zu berechnen. Um dies trotzdem zu erreichen, entwickelten wir unser Didge(R)Evolution-Tool.
Mit diesem Tool werden durch die Anwendung von gerichteten Evolutionsalgorithmen die physikalisch möglichen Formen zur Erreichung der gewünschten Zielspektren aus der extrem großen Vielfalt
möglicher Formen gefunden und Vorschläge für die am besten spielbaren Formen generiert. Für dieses hier gezeigte Beispiel sind kombinatorisch in der verwendeten digitalen Auflösung ca. 1,2x10E144
Formvarianten möglich. Nur zum Vergleich, die Anzahl der Atome im sichtbaren Universum beträgt ca. 1,0x10E88. D.h., Evolutionsalgorithmen sind bei komplexen Aufgabenstellungen extrem
effizient.
Da die jeweils gefundenen Lösungen nicht vorhersehbar sind, ist es in der Regel erforderlich viele alternative Spezifikationen zu testen, die auch zu alternativen Lösungen führen. Aufbauend auf
diesen Lösungen und einer umfangreichen Wissensbasis (die kein Bestandteil der Software ist) erfolgt dann die von außen durch den Spezialisten iterativ gelenkte Lösungsfindung.
Um diesen Prozess zu veranschaulichen, versuche ich, eine typische Vorgehensweise an einem Beispiel zu zeigen.
Es soll die Innenform für ein Yidaki-Typ Instrument mit folgenden Eigenschaften gefunden werden:
- a) Grundton F;
- b) 1. Toot G1 und 2. Toot C2 (beide leicht und stabil anspielbar);
- c) 2.Oberton (3.Harmonische) C2 wenn möglich als Sington ausgeprägt;
- d) Mischton (Heterodyne) aus Stimmton C (Quinte über Grundton F) und Grundton F soll wie bei Mago-Typ Instrumenten unterstützt werden;
- e) Die Obertöne 5, 6 und 7 (Harmonische 6, 7 und 8) sollen je nach Spielweise als Singtöne oder Oberton-Wobbeln (Harmonic-wobbles) anregbar sein;
- f) Das Instrument soll eine gute akustische Elastizität beim Spielen aufweisen;
Auf Basis dieser Wunsch-Spezifikation können nun die erforderlichen physikalischen Parameter abgeleitet werden.
Wichtiger als der Grundton sind alle anderen gewünschten Eigenschaften, da sich diese aus physikalischer Sicht in relativer Relation zum Grundton definieren lassen. Das genaue Einstellen auf den
gewünschten Grundton erfolgt in der Regel als letzter transformativer Schritt. Prinzipiell ist dann die Transformation auf einen beliebigen Grundton möglich. Durch diese proportionale
Transformation wird die Lage des ersten intrinsischen Impedanzpeaks auf die gewünschte Frequenz des Grundtons (in unserem Beispiel auf 87,31 Hz, Grundton F) eingestellt. Dabei bleiben alle
realisierten Eigenschaften erhalten.
Um trotzdem schon in der Nähe des gewünschten Grundtons F zu landen, starten wir die gerichtete evolutive Suche mit einer festen Länge von 153 cm, da aus Erfahrung derartige typische
Yidaki-Instrumente mit Grundton F in diesem Bereich liegen.
Des Weiteren begrenzen wir den Suchbereich der gerichteten Evolution in einem Bereich, in dem natürlicherweise auch Termiten einen vorhandenen Eukalyptus-Stamm ausfressen würden. Für dieses
Beispiel verwenden wir eine Version mit 40 virtuellen Segmenten und insgesamt 80 variablen geometrischen Parametern.
Ableitung der physikalischen Parameter:
- zu a) Grundton F (1. Impedanzpeak bei 87,31 Hz bezogen auf 87,31 Hz -> Verhältnis = 1,00);
- zu b) 1. Toot G1 (2. Impedanzpeak bei 196,00 Hz bezogen auf 87,31 Hz -> Verhältnis = 2,25); 2. Toot C2 (3. Impedanzpeak bei 261,60 Hz bezogen auf 87,31 Hz -> Verhältnis = 3,00); Für eine gute Anspielbarkeit des 1. und 2. Toots sollten die Impedanzpeaks 2 und 3 eine definierte Mindesthöhe haben.
- zu c) Der 2.Oberton (3.Harmonische) C2 sollte durch einen Impedanzpeak bei 261,60 Hz (Verhältnis 3,00 zur Grundtonfrequenz) unterstützt werden. Dieses Ziel ist bereits durch die gewünschte Lage des 2.Toots definiert. Da die Höhe des 2. Impedanzpeaks für eine gute Anspielbarkeit des 2. Toots eine definierte Mindesthöhe haben soll, wird der Sington wahrscheinlich nicht sehr prominent ausfallen. Um dies zu erreichen, sollte dessen Höhe wesentlich geringer ausfallen, was dann allerdings zu einer Verschlechterung der Anspielbarkeit führen würde.
- zu d) Um einen Mischton aus Stimmton einer Quinte über dem Grundton und diesem Grundton zu unterstützen, sind jegliche Frequenzen genau aus dem Mittelwert der jeweils beiden benachbarten Obertonfrequenzen ab der 2.Oktave zum Grundton mit einem Impedanzpeak zu unterlegen. Also an den Frequenz-Verhältnissen 5/2, 7/2, 9/2, 11/2, 13/2, 15/2, 17/2, … (je kleiner die Verhältnisse, um so wirksamer); Also, da die Lage der ersten 3 Impedanzpeaks schon vergeben ist und wir den Mischton (Heterodyne) aus Stimmton C (Quinte über Grundton F) und Grundton F wie bei Mago-Typ Instrumenten unterstützen wollen, legen wir den 4. Impedanzpeak auf das Verhältnis 9/2 = 4,5;
-
zu e) Die Obertöne 5, 6 und 7 (Harmonische 6, 7 und 8) sollen je nach Spielweise als Singtöne oder Oberton-Wobbeln (Harmonic-wobbles) anregbar sein. Dafür unterlegen wir
diese drei Obertöne mit den Impedanzpeaks 5, 6 und 7. Um ein symmetrisches Muster zu erreichen platzieren wir unter den mittleren (zentralen) Oberton 6 den Impedanzpeak 6 und platzieren den
Impedanzpeak 5 ca. 2-3% linksseitig von der Frequenz des Obertons 5 und den Impedanzpeak 7 ca. 2-3% rechtsseitig von der Frequenz des Obertons 7. Dadurch sollte beim stationären Spielen
der Oberton 6 als Sington wahrnehmbar sein und beim traditionellen dynamischen Spiel die Obertöne 5 und 7 wechselseitig zum Oberton-Wobbeln anregbar sein. Um eine gute Wahrnehmung dieser
Obertöne zu erreichen, was durch eine gute Übertragung der Schallenergie dieser Obertöne vom Bellend gesichert wird, darf die Höhe der jeweils unterlegten Impedanzpeaks nicht zu hoch
sein.
Verhältnisse der Impedanzpeaks 5, 6, 7 zum Grundton F 87,31 Hz:
Impedanzpeak 5: ca. 2,5% unter Oberton 5 -> 510,8 Hz / 87,31 Hz -> Verhältnis 5,85
Impedanzpeak 6: Oberton 6 -> 611,2 Hz / 87,31 Hz -> Verhältnis 7,00
Impedanzpeak 7: ca. 2,5% über Oberton 7 -> 711,6 Hz / 87,31 Hz -> Verhältnis 8,15 -
zu f) Durch die um jeweils ca. 2-3% symmetrisch versetzten Impedanzpeaks 5 und 7 in Relation zu den Obertönen 5 und 7 erhält das Instrument bereits eine gute akustische
Elastizität. Diese ist noch zu verbessern, indem die beiden folgenden Impedanzpeaks 8 und 9 ebenfalls um jeweils ca. 2-3% linksseitig vom Oberton 8 (Harmonische 9) und ca. 2-3% rechtsseitig
vom Oberton 9 (Harmonische 10) platziert werden. Aus Gründen der besseren Hörbarkeit und Stimmenübertragung in diesem hohen Frequenzbereich werden die unterlegten Impedanzpeaks auch in ihrer
Höhe begrenzt.
Verhältnisse der Impedanzpeaks 8, 9 zum Grundton F 87,31 Hz:
Impedanzpeak 8 ca. 2% unter Oberton 8 -> 855,6 Hz / 87,31 Hz -> Verhältnis 9,80
Impedanzpeak 9: ca. 2% über Oberton 9 -> 977,9 Hz / 87,31 Hz -> Verhältnis 11,20
Um diese von der Spezifikation abgeleiteten physikalischen Parameter quantitativ in die Algorithmen der gerichteten evolutiven Suche zu überführen (bereit zu stellen), stehen momentan 19 Funktionen zur Zieldefinition zur Verfügung.
Diese Bereitstellung führt zu den folgenden 15 Suchzielen für die gerichtete Evolution, denen noch als zusätzliches Ziel die Minimierung der gewichteten Summe der Winkel zwischen den Segmenten zugefügt ist. Durch dieses zusätzliche Ziel wird aus den theoretisch unendlich vielen Lösungsmöglichkeiten immer die „glatteste“ Innenform ausgewählt, die aus Erfahrung auch meist die beste Spielbarkeit aufweist.
In der momentan verwendeten Version der Directed-Evolution sind bis zu 20 parallele Suchziele möglich.
Run einer Directed-Evolution:
Da die wenigsten Didgeridoo-Bau-Interessierten sich mit mathematischer Modellierung, Programmierung und physikalischen Theorien auskennen, hier eine vereinfachte Beschreibung der Arbeitsweise:
- Stellt Euch vor, wir erschaffen (programmieren) virtuelle Termitenvölker, deren Einzeltermiten individuelle Fähigkeiten besitzen, Didgeridoos mit speziellen Eigenschaften zu formen. Im ersten Schritt wird die Größe und Anzahl dieser virtuellen Termitenvölkern festgelegt. In unserem Bespiel arbeiten wir lediglich mit einem Volk (Population) bestehend aus 512 Termiten (Individuen).
- Innerhalb der räumlichen Begrenzung des virtuellen Rohlings (des Suchbereiches) nimmt jede einzelne Termite ihre Arbeit auf und frisst (erstmal völlig zufallsgesteuert) ihr eigenes Didgeridoo aus. Nach einigen Sekunden sind die ersten 512 virtuellen Instrumente fertig.
- Nun wird jedes einzelne Instrument auf Basis der simulierten/berechneten Impedanz- und Klangspektren daraufhin überprüft, wie gut es die vorgegebenen Ziel-Eigenschaften erfüllt. Die Termiten, die am erfolgreichsten waren, dürfen sich vermehren und ihre Erbinformationen an eine neue Termitengeneration weitergeben. Die anderen sterben aus. D.h., die erfolgreichsten virtuellen Instrumente bleiben im Pool erhalten und werden als Ausgangsinstrumente für die Modifikationen der weiteren Formen verwendet. Zusätzlich werden, ähnlich wie in der Natur, zufällige Mutationen erzeugt, die die individuellen Eigenschaften von einzelnen Termiten (Instrumenten) ändern. Damit ist die erste Generation beendet.
- In der zweiten Generation fressen die Sprösslinge zusammen mit ihren relativ erfolgreichen Eltern und den mutierten Geschwistern erneut 512 Didgeridoo-Rohlinge aus – wieder zufallsgesteuert aber mit verbesserten Eigenschaften die Zielvorgaben zu erreichen. Dahinter verbergen sich eine Reihe verschiedener mathematischer Operatoren, die nach den bekannten Gesetzen z.B. der genetischen Algorithmen, die vorhandenen Informationen so mischen und rekombinieren, dass eine neue Generation an virtuellen Instrumenten entsteht, die statistisch mit hoher Wahrscheinlichkeit zu einer besseren Erfüllung der Zielvorgaben führen sollten.
- Danach werden wieder sämtliche Instrumente überprüft. Die erfolgreichen Termiten (virtuellen Instrumente)des Volkes (Instrumenten Pools) dürfen sich wiederum vermehren, während der Rest ausstirbt (wie in vorhergehender Generation bereits beschrieben).
- Dieser evolutionäre Kreislauf setzt sich so lange fort, bis ein virtuelles Didgeridoo erzeugt wurde, das alle vorgegebenen Ziele bestmöglich erfüllt und es keinen evolutionären Fortschritt mehr gibt – im Beispiel sichtbar als rote Linie. In der Regel ist das nach 150 bis 400 Generationen der Fall. Die aktuell typische Zeit für einen modernen Einzelprozessor beträgt dafür 10-30 min.
Um die directed Evolution nicht durch zu viele Ziele festzufahren, startet man in der Regel mit weniger Zielvorgaben, die dann schrittweise auf Basis der beobachteten Evolution und eigenen
Erfahrungen immer weiter auf die Gesamtziele erweitert werden. Da der Überwacher der directed Evolution (in diesem Fall ich) die Entwicklung der Resultate graphisch verfolgen kann, werden die
schrittweisen Erweiterungen bzw. Modifikationen schon während aktiver Runs vorbereitet und parallel zu den schon laufenden Runs gestartet. Runs, die nicht erfolgversprechend laufen, werden
abgebrochen. In dieser Phase sind mit meiner aktuellen Technik bis zu ca. 30 paralleler Runs auf 30 Prozessoren möglich. D.h., vor allem bei komplizierten Projekten bin ich momentan noch ein
essentieller Teil dieser globalen Optimierung mit Hilfe der gerichteten künstlichen Evolution. Da jede globale Suche anders und oft unvorhersehbar läuft, bleibt dieser Prozess bis heute
spannend.
Dabei ergeben sich typische Entwicklungszeiten von ca. einer Stunde für einfachere Projekte, bis zu 2 mehreren Tagen für komplizierte komplexe Projekte auch mit automatischen Runs über Nacht. Ist
einmal die beste und physikalisch geeignete Zielkombination gefunden, laufen dann die letzten Runs oft mit mehreren Tausend Generationen, um aus der Vielzahl möglicher Formen nach aktuellen
Erfahrungsstand die Beste zu finden. In unserem Beispiel sind es jeweils 2200 Generationen.
Alle Varianten der von mir verwendeten Tools bestehen aktuell aus ca. 30000 Zeilen Quell-Code, davon ca. 20000 Zeilen für die Suche mittels gerichteter künstlicher Evolutionsalgorithmen und ca.
10000 Zeilen für die nachträgliche manuelle Modifikation im Didge-Creator.
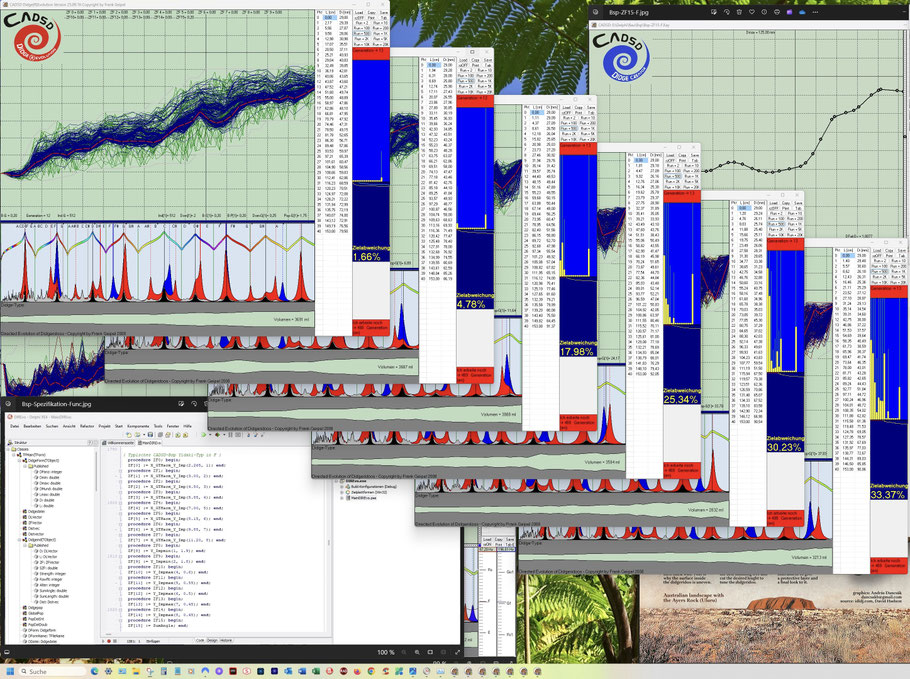
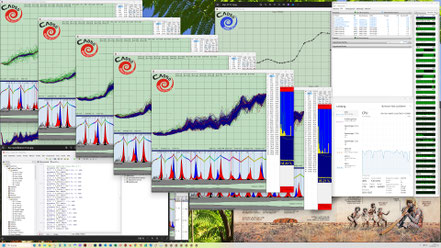
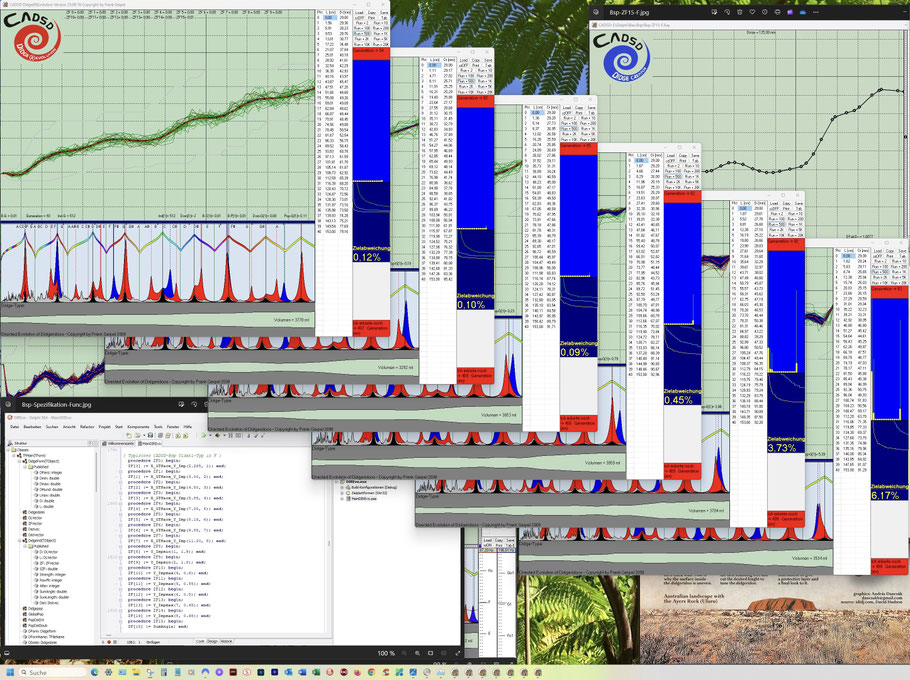
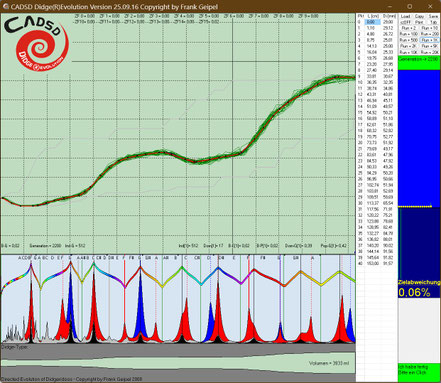
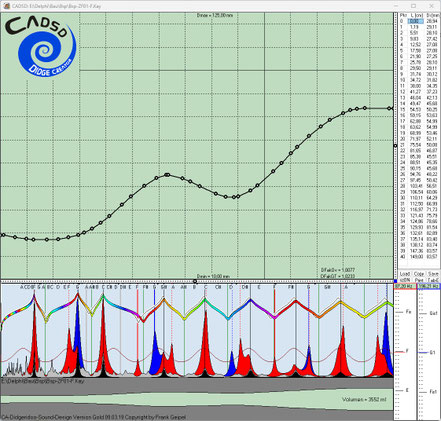
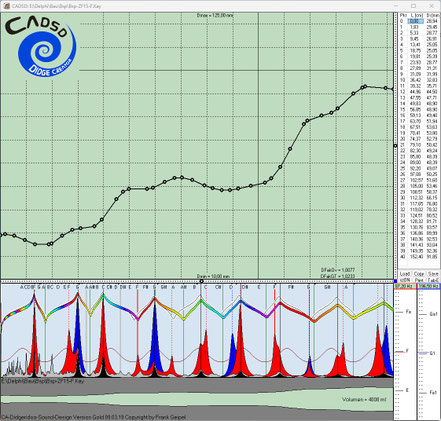
Hier einige Screenshots während der Runs unseres beschriebenen Beispiels:
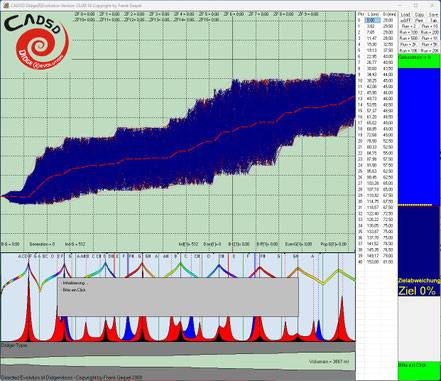
Hier wurden 6 Evo-Runs parallel gestartet, wobei von links nach rechts sich die Anzahl der definierten Einzelziele von 2, 3, 4, 7, 9 bis 16 steigert. Die Höhe der gelben Einzelbalken gibt graphisch einen Eindruck, wie weit ein Einzelziel noch von seiner vollständigen Erreichung entfernt ist.
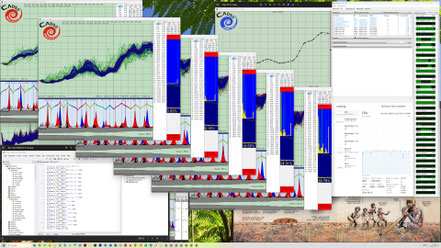
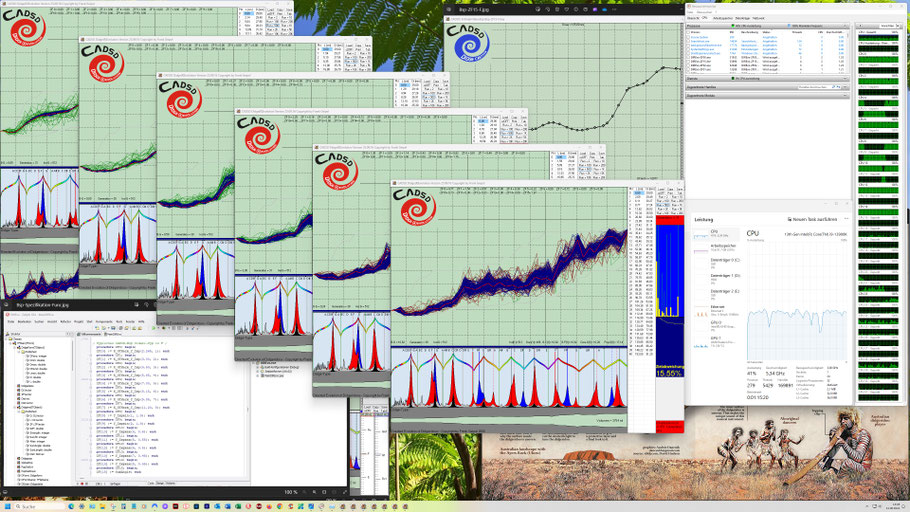
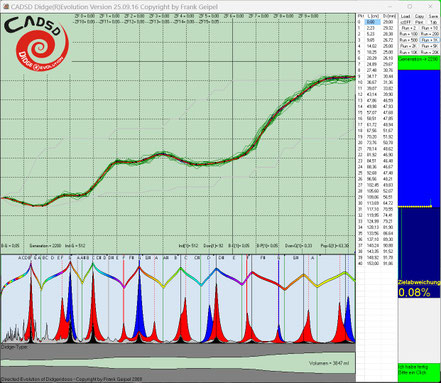
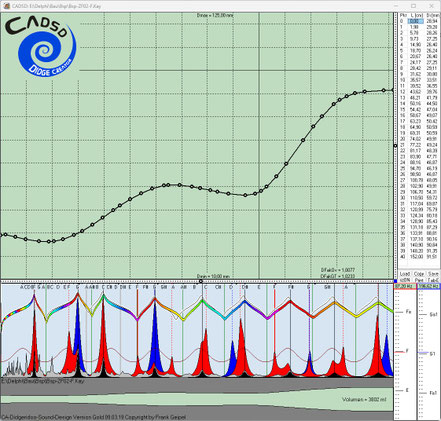
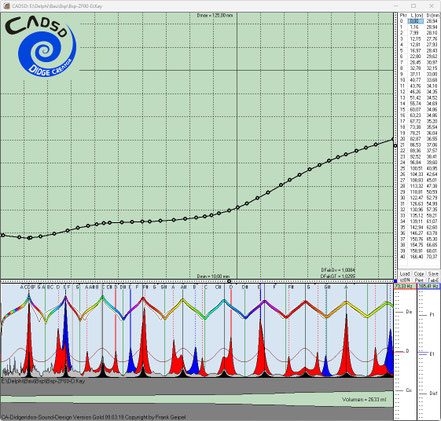
Hier die gleichen Evo-Runs einige Generationen weiter:
Die in den dunkelblauen Fenstern nach links abfallenden dünnen Kurven (gelb, hellblau und grün) zeigen jeweils in zwei Zehnerpotenz-Abständen die Annäherung bzw. Konvergenz auf das Gesamtziel
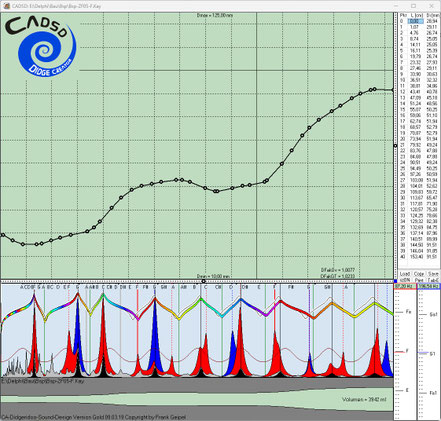
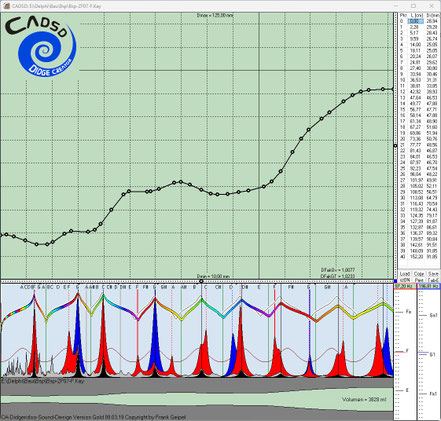
Null-Abweichung. In den folgenden Screenshots kann man erkennen, je mehr Einzelziele und komplexer diese sind, desto langsamer konvergieren die Evo-Runs zum Gesamtziel Null-Abweichung.
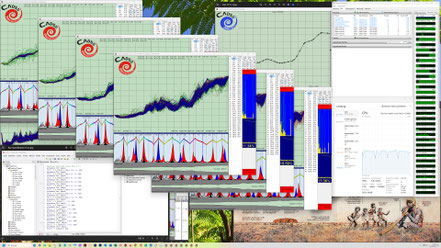
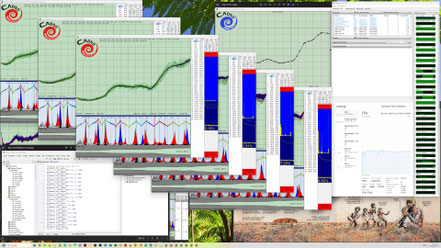
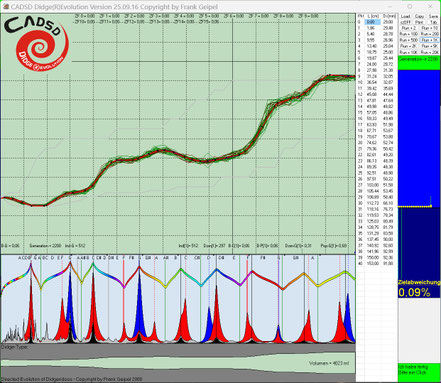
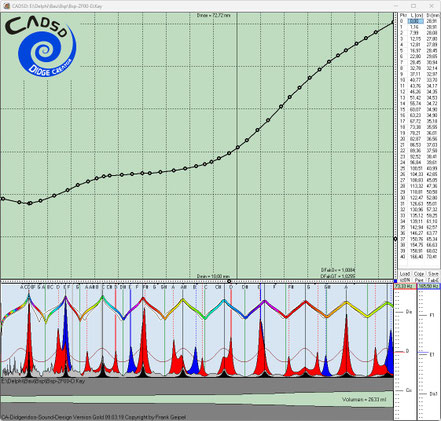
Falls sich die Einzelziele widersprechen oder physikalisch nicht erreichbar sind, konvergiert der jeweilige Evo-Run bei einer relativ großen von Null verschiedenen Restabweichung. In diesem
Beispiel gibt es durch die Erfahrungs-basierte Zieldefinition für jeden Evo-Run eine Lösung.
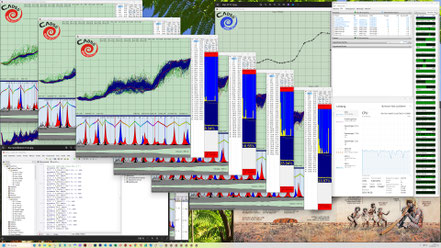
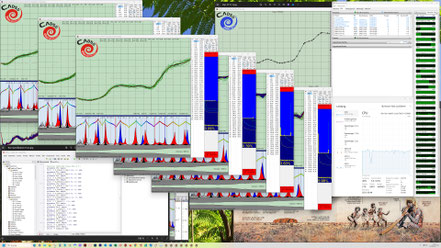
Hier kann man die in den dunkelblauen Fenstern nach links abfallenden dünnen Kurven (gelb, hellblau und grün) besser erkennen. Diese zeigen jeweils in zwei Zehnerpotenz-Abständen die Annäherung bzw. Konvergenz auf das Gesamtziel Null-Abweichung. Je mehr Einzelziele und komplexer diese sind, desto langsamer konvergieren die Evo-Runs zum Gesamtziel Null-Abweichung.
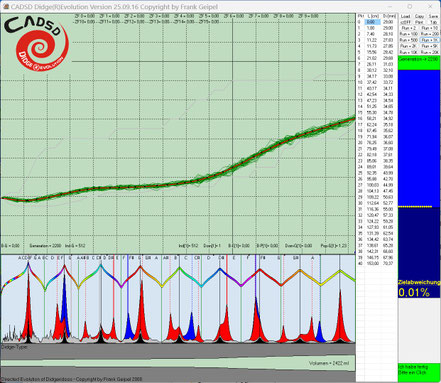
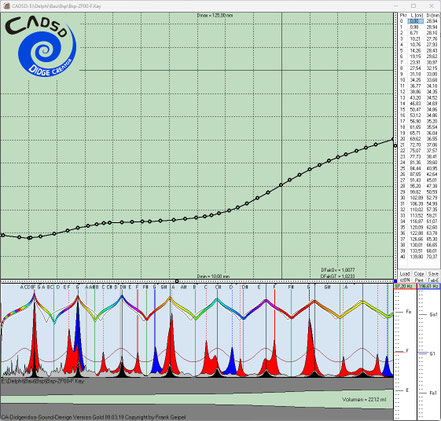
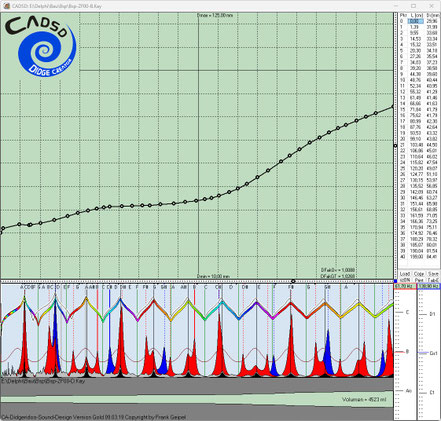
Diskussion der Einzelergebnisse der Evo-Runs 1-6 nach jeweils 2200 Generationen:
Evo-Run 1 -> 2 Ziele
Obwohl hier nur zwei Ziele definiert waren, ergab sich in diesem Run ein sehr interessantes Instrument. Wahrscheinlich deshalb, weil in diesem Run der minimal zugelassene Belldurchmesser auf
70 mm begrenzt war.
Neben dem 1.Toot, der einen ganzen Ton über der Oktave liegen sollte, hat dieses Instrument noch folgende Zusatzqualitäten:
Durch die Lage des 3. Impedanzpeaks bei einem Frequenzverhältnis von 3,5 zum Grundton, sind hier die Mischtöne aus Stimmton (Quinte über Grundton) und Grundton wie bei Mago-Typ Instrumenten
unterstützt.
Des Weiteren sollte der 4. Oberton (5. Harmonische) durch die Unterlagerung des 4. Impedanzpeaks deutlicher als Sington (für geübte Hörer) wahrnehmbar sein.
Und als ungeplante Zugabe hat sich noch ein Oberton-Wobbel-Muster mit den beiden Obertönen 7 und 8 (Harmonische 8 und 9) durch die symmetrisch versetzte Unterlagerung der Impedanzpeaks 6 und
7 ergeben.
Derartige Zufälle sind eher selten, aber umso erfreulicher für die möglichen Interessenten an diesem Beispiel.
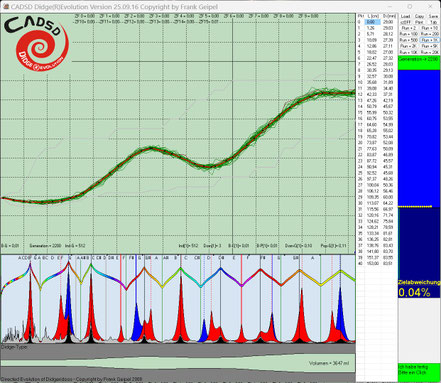
Evo-Run 2 -> 3 Ziele
Obwohl hier nur drei Ziele definiert waren, ergab sich auch in diesem Run ein sehr interessantes Instrument. Neben dem 1.Toot, der einen ganzen Ton über der Oktave liegen sollte und dem
2.Toot genau auf der dreifachen Frequenz des Grundtons hat dieses Instrument noch folgende Zusatzqualitäten:
Der 5. Oberton (6. Harmonische) sollte durch die Unterlagerung des 5. Impedanzpeaks deutlicher als Sington (für geübte Hörer) wahrnehmbar sein.
Auch hier haben sich einige symmetrische Muster ergeben, die zu einer guten akustischen Elastizität beim Spielen mit bestimmten Techniken spürbar sein sollten.
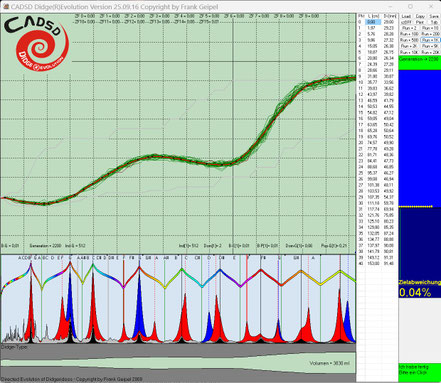
Evo-Run 3 -> 4 Ziele
Obwohl hier nur vier Ziele definiert waren, ergab sich auch in diesem Run wieder ein sehr interessantes Instrument. Neben dem 1.Toot, der einen ganzen Ton über der Oktave liegen sollte, dem
2.Toot genau auf der dreifachen Frequenz des Grundtons und des Impedanzpeaks bei der 4,5fachen Frequenz des Grundtones, der zur Unterstützung von Mischtönen aus Stimmton (Quinte über Grundton)
und Grundton wie bei Mago-Typ Instrumenten führen sollte, hat dieses Instrument noch die ungeplante Zusatzqualität eines Oberton-Wobbel-Musters mit den beiden Obertönen 5 und 6 (Harmonische 6 und
7) durch die symmetrisch versetzte Unterlagerung der Impedanzpeaks 5 und 6.
Wenn man genau auf die Ergebnisse schaut, kann man erkennen, dass die angepeilten Ziele alle relativ zum ersten Impedanzpeak (dem Grundton) erreicht wurden, aber die Frequenz dieses ersten
Impedanzpeaks noch auf die gewünschte Grundtonfrequenz F auf 87,31 Hz eingestellt werden müssen. Dies war zu erwarten und ist normal, da die Grundtonfrequenz nicht nur von der Länge abhängt (in
diesem Fall 153 cm), sondern von der gesamten Innenformgeometrie des Instrumentes.
Für diese Anpassungen, Transformationen und Feinabstimmungen verwenden wir den Didge-Creator.
4. Transformation mit dem Didge-Creator:
Vorweg gilt es zu beachten, dass die Höhe des einzustellenden Grundtons auch von einigen Parametern abhängig ist. Zum einen sind das vom Spieler unabhängige physikalische Parameter wie Temperaturgradient und Luftfeuchte im Instrument. Schon dadurch können sich Abweichungen von bis zu einem halben Ton ergeben. So macht es einen deutlichen Unterschied, ob man in den Tropen bei >30°C und maximaler Luftfeuchte oder in einer gemäßigten Zone bei 18°C und geringerer Luftfeuchte spielt. Wobei der Einfluss der Temperatur größer als der der Luftfeuchte ist. Alles im Allen hat dieser Einfluss keine Auswirkungen auf die Gesamtcharakteristik des Instrumentes, da durch die veränderte Schallgeschwindigkeit im Instrument alle relevanten Größen gleich beeinflusst werden und die davon verursachten Änderungen nur relativ sind.
Zum anderen gibt es da noch die vom jeweiligen Spieler individuell abhängigen Parameter. Hierzu gehören der Lippenansatz am Mundstück und damit verbunden die Lippenspannung und der Spieldruck. Auch dadurch kann je nach Instrumenten-Innenform die Grundtonfrequenz bis zu einem Viertelton schwanken. Geübte Spieler verwenden auch bewusst diese Effekte, um z.B. den Grundton bis zu einem Ganzen Ton zu variieren. Bezüglich bestimmter Obertoneffekte (z.B. Singtöne, Harmonic Wobbles) sind diese Abhängigkeiten kritischer zu bewerten, da diese die Gesamtcharakteristik des Instrumentes beeinflussen. So ist dies auch einer der Hauptgründe, warum relativ viele Spieler potentiell vorhandene Sington- bzw. Harmonic-Wobble-Qualitäten nicht zur Entfaltung bringen. In diesen Fällen wäre es erforderlich, über ein Feintuning des Instrumentes dieses so an den Spieler anzupassen, dass diese Effekte für den individuellen Spieler anregbar sind.
Ein weiterer Grund für die Wahrnehmung bzw. Nichtwahrnehmung bestimmter Obertoneffekte ist sie Schulung der eigenen akustischen Wahrnehmung. Das kann man erlernen und üben. Aber ähnlich wie bei anderen Tätigkeiten, gibt es eben Menschen, die ein besonders ausgeprägtes Talent dafür haben und andere weniger.
Einer der wichtigsten Voraussetzungen z.B. für das Anregen potentiell möglicher Harmonic-Wobbles ist allerdings das Beherrschen einer dafür geeigneten Spieltechnik und damit der bewussten Interaktion mit dem Instrument. Dafür besonders geeignet sind die verschiedenen traditionellen Spieltechniken in Balance mit dem Instrument.
So interessant und unterhaltend auch modernere Spieltechniken wie z.B. das Beatboxing sind, führen diese Techniken meist zur akustischen „Vergewaltigung“ eines Instrumentes, wobei damit die akustischen Eigenschaften des Instrumentes nicht mehr diese wichtige Rolle spielen, da hier der Spieler der wichtigste klangerzeugende Aspekt ist und damit ein relativ beliebiges Rohr oft ausreicht.
Leider fallen die meisten Slide-Instrumente auch in diese Kategorie. Diese haben den Vorteil für Musiker in jeder beliebigen Situation den Grundton anpassen zu können. Allerdings ändert sich bei jeder Einstellung auch die Gesamtcharakteristik dieser Instrumente. Das führt dazu, dass meist für geübte Spieler und Hörer nur eine Einstellung für einen akustischen „Sweet Spot“ existiert, was bei deren typischen Einsatz aber den meisten Hörern wahrscheinlich nicht auffallen wird.
Transformation von Instrumenten in andere Tonlagen:
Da sich bei dem Instrument aus Evo-Run 1 einige ungeplante Zusatzqualitäten ergeben haben, zeige ich an diesem Instrument die Vorgehensweise.
Schlussbemerkung:
Das war jetzt viel Stoff für Hard-Core-Didge-Physik-Enthusiasten. Ich hoffe, dass die an diesem Thema interessierten Menschen einen Einblick in das, was ich mit CADSD so treibe, erhalten haben und ich damit einige offenen Fragen beantworten konnte.
Mit herzlichen Grüßen
Frank Geipel 16. Juni 2024