Der Einfluss des Materials auf den Didgeridoo-Klang /  23.04.2023

Trotz der bereits auf dieser Website beschriebenen Erkenntnisse gibt es unter Didgeridoospielenden und -bauenden eine von unzureichenden Grundannahmen und Überzeugungen gekennzeichnete immer wieder aufkeimende Diskussion darüber, welche Auswirkungen die Wahl verschiedener Materialien auf den Klang des Didgeridoo hat. Um zunächst eine Diskussionsgrundlage zu schaffen, können zu diesem Zweck softwarebasierte Analysen und Simulationen durchgeführt werden, wie exemplarisch der folgende Gastbeitrag des bekannten italienischen Ingenieurs und Didgeridoo-Entwicklers Andrea Ferroni zeigt.

Der Beitrag ist ein Auszug aus dem Buch THE DESIGN OF DIDGERIDOO von Andrea Ferroni, 2023, übersetzt und an die Webseite www.didgeridoo-physik.de angepasst von Frank Geipel / Ansgar Stein.

GEKOPPELTE FLUIDDYNAMISCHE INTERAKTIONSANALYSE:
BEWERTUNG DES MATERIALEINFLUSSES AUF DEN KLANG

Andrea Ferroni

Die folgende Analyse wurde durchgeführt, um Enthusiasten und Instrumentenbauenden die Bedeutung der einzelnen Variablen zu verdeutlichen, die bei der Gestaltung eines Didgeridoos eine Rolle spielen.

Für diese Analyse wurden zwei Formen betrachtet:

Abbildung 1: LSD IV-Form

Die Form LSD IV (Large Spectrum D, IV Variante), ist die vierte Überarbeitung einer Instrumentenform in D, die erstmals 2003 realisiert wurde und deren Klangfarbe durch das Vorhandensein von mehreren harmonischen und unharmonischen Komponenten gekennzeichnet ist, die typisch für Formen sind, die unregelmäßigen Konen ähneln. Das Intervall zwischen dem Grundton und der nächst höheren Eigenresonanz der Luftsäule (1. Toot) beträgt genau eine Oktave.

Abbildung 2: Open Didgeridoo-Form

Die Form Open Didgeridoo, ebenfalls in D, mit einem Intervall zwischen dem Grundton und der nächst höheren Eigenresonanz der Luftsäule von einer großen Terz oberhalb einer Oktave des Grundtons. Diese zweite Form stellt einen Kompromiss dar zwischen einer zylindrischen und einer konischen Form. Sie ergibt ein klareres Timbre, da die Resonanzen weiter auseinander liegen als bei einem konischen Instrument. Gleichzeitig ist ihr Timbre reicher als bei einem perfekt zylindrischen Instrument. Letztlich lässt diese Eigenschaft die Klangfarbe heller erscheinen, da aufgrund der geringeren Präsenz im Bereich von ca. 50-700 Hz die durch die Veränderung des Vokaltraktes des Spielers betonten Obertöne mit einer Frequenz oberhalb von 500 Hz deutlicher hervortreten und so eine Brillanz bewirken.

Im Folgenden eine Zusammenfassung der kombinierten und untersuchten Varianten:

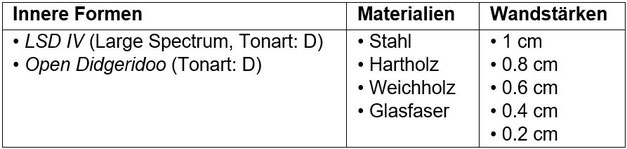
Abbildung 3: Zusammenfassung der in dieser Studie verwendeten und kombinierten Varianten

Mit ACTRAN werden die Hohlraummoden der Luftsäule mit den Moden und Resonanzen des Instrumentenkörpers gekoppelt, um mögliche Wechselwirkungen zwischen Luft und Festkörper zu bewerten.
In einer ersten Modalanalyse werden die Resonanzfrequenzen des Instrumentenfestkörpers simuliert und die Bereiche, in denen Verformungen auftreten, bei jeder Frequenz bis zu 1000 Hz bewertet.
Anschließend werden, ähnlich wie bei anderer 1D-Simulationssoftware, die Eigenresonanzfrequenzen des Hohlraums (der schwingenden Luftsäule) und die Bereiche, in denen Druckänderungen aufgrund stehender Wellen auftreten, ebenfalls in einem Frequenzbereich von bis zu 1000 Hz simuliert.

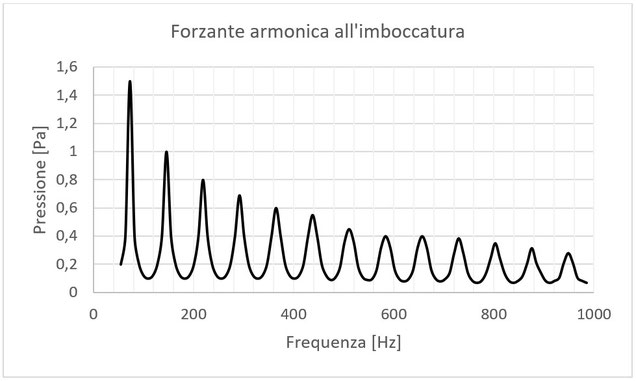
Abbildung 4: Grafische Darstellung der Druckanregung im Frequenzbereich von 0-1000 Hz

Von hier an greift die eigentliche Spezialisierung von ACTRAN:
Das geschlossene Ende des Didgeridoos, am Mundstück, wird mit Druckvariationen beaufschlagt, die der Vibration der Lippen eines Spielers ähneln – periodische, harmonische Druckschwankungen, die Maxima bei dem perfekten Grundton des Instruments D und all seinen natürlichen Obertönen ergeben:

Abbildung 5: Position der simulierten Messstellen (gelb);

Eine Reihe von Messstellen (simulierte Messmikrofone) wurden 5 cm vom Korpus des Instruments entfernt platziert/simuliert. Das erste in der Nähe des Mundstücks, das zweite auf halber Höhe, ein drittes auf ¾ der Länge des Instruments und ein letztes vor der Schallöffnung, wie es normalerweise bei einer Aufnahme oder einem Konzert platziert wird.

Es zeigte sich, dass die Simulationsergebnisse der verschiedenen Messstellen extrem ähnlich sind und sich quasi nur durch die Intensität unterscheiden. Je größer die Entfernung vom Bellend um so bis -20dB geringer die Intensität. Aufgrund dieser Ergebnisse wird nur die 5 cm von der Schallöffnung entfernte simulierte Messstelle weiter berücksichtigt. Da der Schwerpunkt dieser Analyse die Bewertung des Materialeinflusses auf den Klang ist, werden ebenfalls nur die Ergebnisse der verschiedenen Materialien bei 1 cm Wandstärke weiter analysiert.

Auf meinem persönlichen PC (Intel®Core™ i7-8700 CPU @ 3.20GHz, 24GB RAM), dauerte die Berechnung einer Kurve für jedes oben beschriebene simulierte Messmikrofon etwa 40 Minuten, für jede einzelne Material- oder Wandstärkevariation.
Die ersten vier Durchläufe zur Untersuchung von vier Materialien — Stahl, Hartholz, Weichholz, Glasfaser — sind folgend dargestellt:

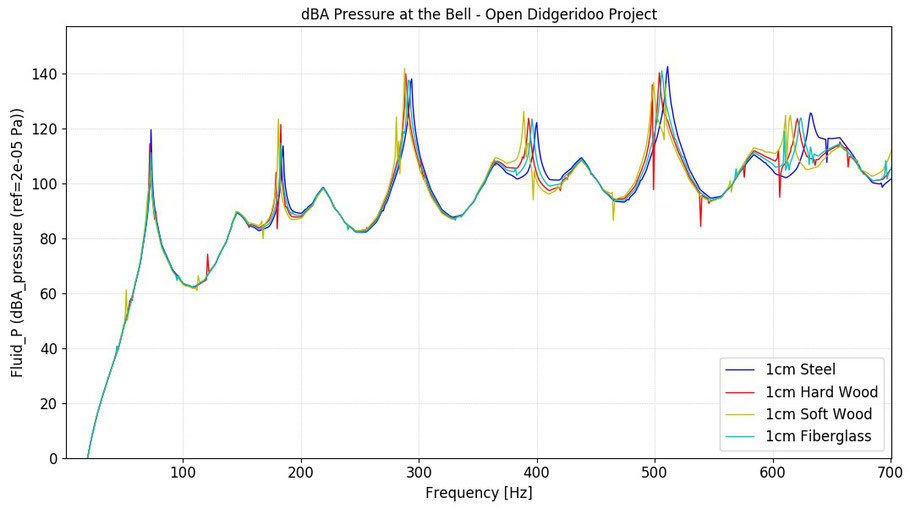
Abbildung 6: Druck in dBA in 5 cm Entfernung von der Schallöffnung. Die verschiedenen Farben stehen für die 4 betrachteten Materialien.

Die Kurvenprofile sind hier über den gesamten Frequenzbereich überlagert dargestellt. Der größte Unterschied, der sich feststellen lässt, ist eine zunehmende Abweichung in den Resonanzfrequenzen bei steigender Frequenz.
Zwischen Stahl und Weichholz beträgt die Differenz 12 Hz bei etwa 500 Hz (499 Hz für ein Weichholz - Instrument, im Vergleich zu 511 Hz für ein identisches Stahlinstrument). Bedenkt man, dass in diesem Frequenzbereich in der temperierten Tonleiter (A auf 440 Hz gestimmt), B4 bei 493,88 Hz und C5 bei 523,25 Hz mit einem Halbton-Abstand von 29,37 Hz liegen, beträgt die tonale Differenz aufgrund der Materialveränderung weniger als 25 Cent für die 7. Harmonische. Diese Differenz reduziert sich auf weniger als 5 Hz zwischen Hart- und Weichholz und auf weniger als 2 Hz zwischen Hartholz und Glasfaser und liegt damit unter der menschlichen Wahrnehmungsschwelle von ca. 5 Cent.

Ein ähnliches Ergebnis erhält man bei der zweiten Form:

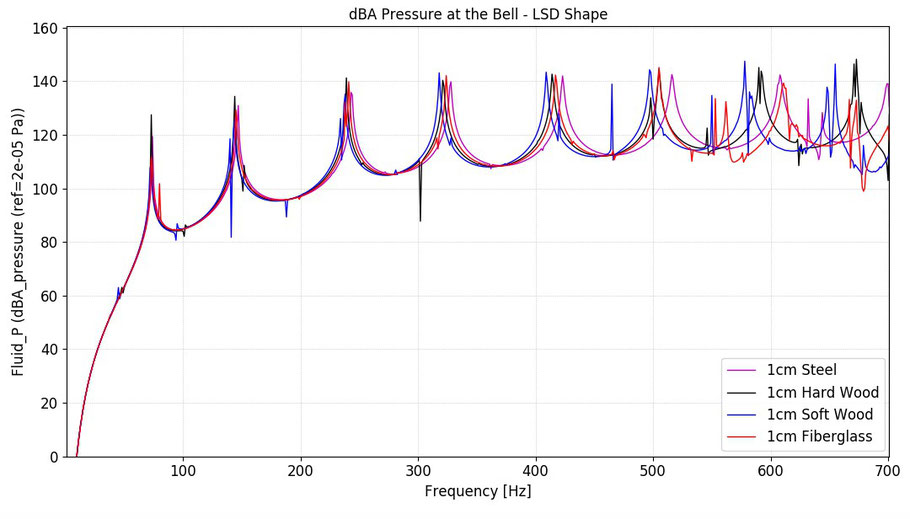
Abbildung 7: Schalldruck in dBA in 5 cm Entfernung von der Schallöffnung mit denselben vier Materialien bei geänderter Form

Sehen wir uns nun den Vergleich der beiden oben analysierten Formen an:

Abbildung 8: Überlagerung der untersuchten Formen

Die Unterschiede zwischen dem Open Didgeridoo (einer Open Source-Form) und der LSD IV Form sind in einem Durchmesser zu finden, der auf dem ersten 80 cm-Abschnitt des Open Didgeridoo um 2 mm um 2 mm größer und zylindrischer ist als bei der LSD IV Form. Auf einer Länge von 80 bis 150 cm weist das Open Didgeridoo eine kleine Volumenerweiterung auf, die die zweite Resonanz auf eine große Terz oberhalb einer Oktave der Grundtonfrequenz bringt und wird dann bis zum Ende des Instruments breiter, wobei ein Schalltrichter mit moderatem Durchmesser erhalten bleibt. Im Gegensatz dazu weitet sich die LSD IV Form auf einer Länge von 80 bis 170 cm auf und endet dann in einem Zylinder von etwa 13 cm Länge, wobei eine deutlich größere Gesamtlänge notwendig ist, um dieselbe Grundtonfrequenz wie bei der vorigen Form zu erhalten.

Folgend ein Vergleich der simulierten Spektren der beiden Instrumentenformen mit demselben Material:

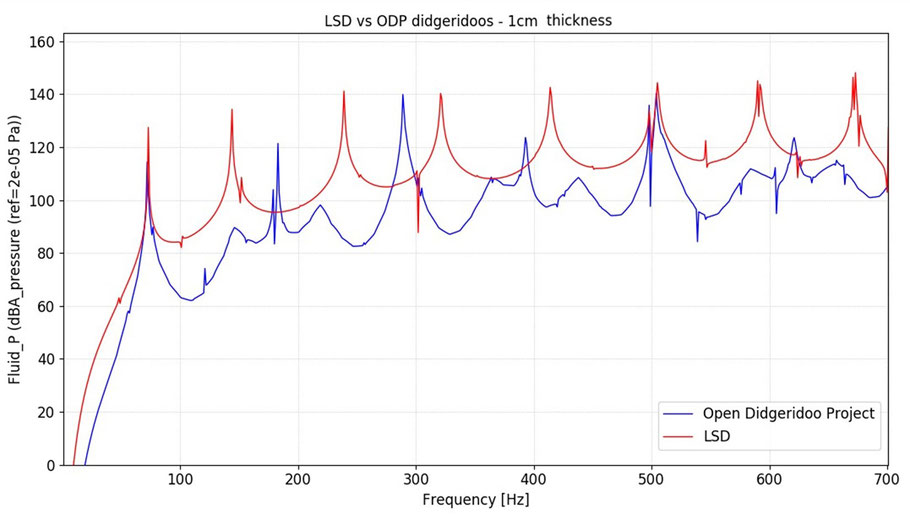
Abbildung 9: Überlagerung der Schallintensitäten der beiden Formen bei Verwendung desselben Materials, mit einem Abstand des simulierten Messmikrofons von 5 cm zur Schallöffnung

In diesem Fall kann man zwei sehr unterschiedlichen Spektren erkennen. So unterschiedlich, dass man denken könnte, es handele sich um die Stimmen von unterschiedlichen Personen und deren Aussprache verschiedener Vokale, oder sogar um die Spektren verschiedener Instrumentenfamilien, denn bei isolierter Betrachtung der beiden übereinstimmenden Grundtöne bieten die verschiedenen harmonischen und unharmonischen Klangkomponenten sehr unterschiedliche Timbres.

Eine andere Ausgabemöglichkeit von ACTRAN ist eine Darstellung zur Prognose der Schallabstrahlung im 360°-Raum. In der folgenden Abbildung 10 wird die Verteilung der Schallintensität in dBA innerhalb und außerhalb des Instrumentes in einer Raumkugel mit 2 m Radius dargestellt:

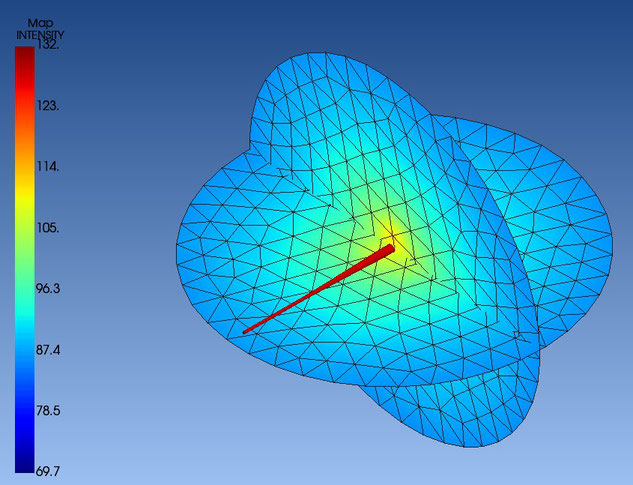
Abbildung 10: Bei einem Grundton von 73 Hz sieht man in Rot das Innere des Instruments mit ca. 130 dB, bis hinunter auf ein Minimum von 69,7 dB außerhalb der 2 m Raumkugel

Eine weitere Ausgabemöglichkeit von ACTRAN ist die Verteilung des Schalldrucks, die in den nächsten Abbildungen zu sehen ist. Während bei der Schallintensität ein Abklingen mit dem Entfernen von der Instrumentenöffnung zu beobachten ist (das Geräusch wird leiser), sehen wir bei den Druckwellen eine periodische Abfolge von Druckmaxima und Druckminima (unter der Annahme, dass der atmosphärische Druck 0 beträgt) und diese verringern sich bei abnehmender Schallintensität. Das ist dadurch begründet, dass sich die Schallenergiedichte auf einer 360°-Kugeloberfläche verteilt (verdünnt), die mit dem Quadrat der Entfernung zur Schallquelle zunimmt.

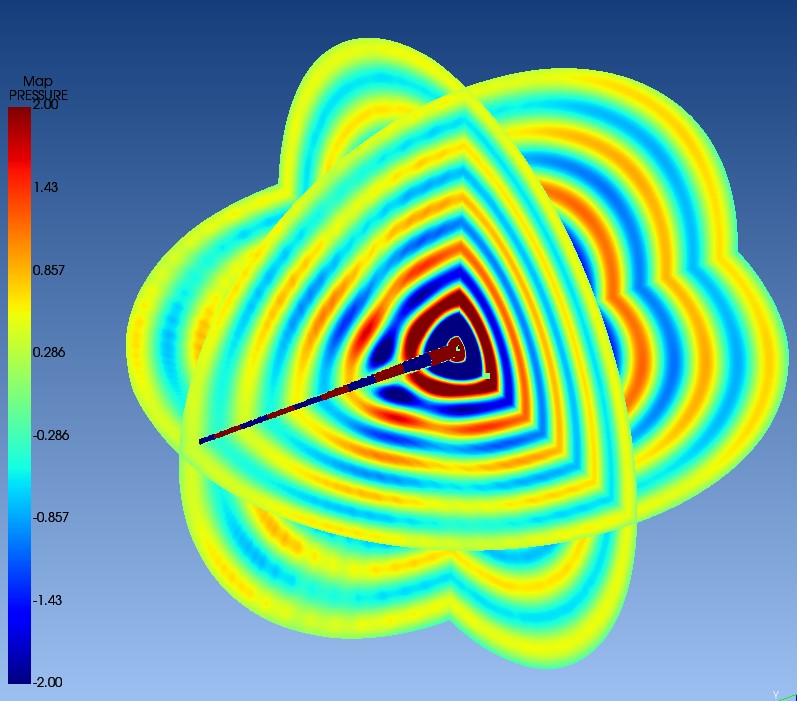
Abbildung 11: Druckverteilung, die sich beim Anblasen der 5. Eigenresonanzfrequenz (4. Toot) ergibt

Während für die Simulation und Darstellung der Schallintensität ein grobes Finite-Elemente-Raster ausreicht (siehe das Gitter in Abbildung 10), musste für die Simulation und Darstellung des Schalldrucks ein wesentlich dichteres, feineres Finite-Elemente-Raster verwendet werden, um das sinusförmige Muster in einer verbesserten Auflösung zu erfassen. Dieses Raster ist so dicht, dass es zur besseren graphischen Lesbarkeit ausgeblendet wurde.
Im Instrumentenkörper sind deutlich die fünf sich positiv und negativ abwechselnden Druckbereiche zu erkennen, die typisch für die stehenden Wellen der gespielten fünften Eigenresonanz (4. Toot) einer halbgeschlossenen Röhre sind.

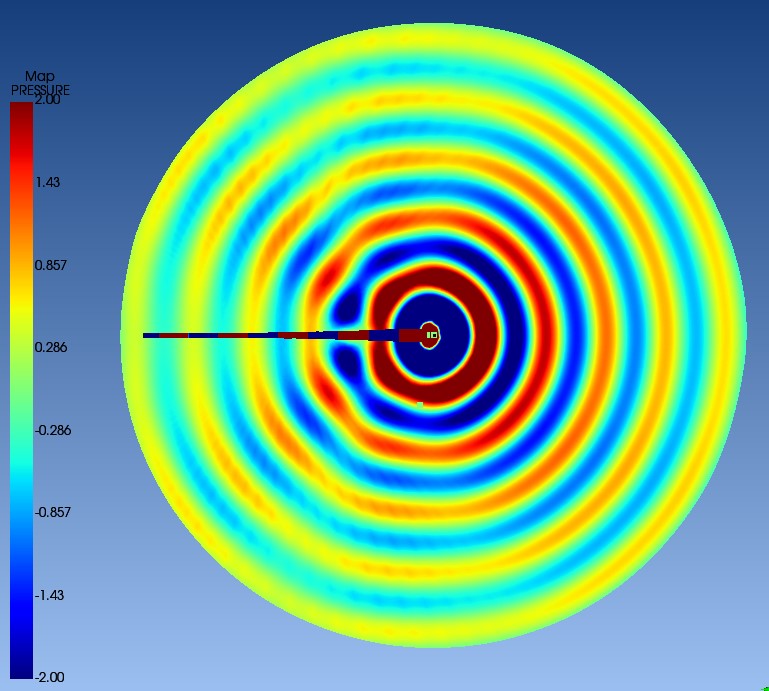
Abbildung 12: Ansicht in der XY-Ebene, die die Ausbreitung der Schalldruckwellen im Raum zeigt.

Falls die Eigenschwingungen bzw. Eigenresonanzen des vibrierenden Instrumentenkörpers einen signifikanten Schalldruck erzeugen würden und damit Einfluss auf den abgestrahlten Klang hätten, würden ausgehend von diesen Stellen eine Reihe signifikanter konzentrischer Druckwellen entstehen. Diese würden mit den aus der Schallöffnung kommenden Druckwellen kollidieren und dadurch deutliche Interferenzmuster erzeugen. Dies ist aber nur minimalst erkennbar. Man sieht lediglich die (durch die stehende Welle der Luftsäule im Instrument) auf den Instrumentenkörper aufgezwungene geringe Übertragung der stehenden Welle im Instrument. Aber diese hat keinen signifikanten Einfluss auf das abgestrahlte Klangfeld und ist deshalb wahrscheinlich in den meisten Fällen vernachlässigbar.

Personal website: www.andreaferroni.it
Didgeridoo outreach site: www.didgeridoo.it 
Didgeridoo research site: www.windproject.it 
YouTube: www.youtube.com/@AndreaFerroni 
Mail: info@andreaferroni.it

Kommentar von Frank:

Es ist immer wieder eine Freude, interessante neue Beiträge zum Thema Didgeridoo von enthusiastischen Menschen wie Andrea Ferroni auf dieser Website zu präsentieren. Vor allem, um die Plausibilität, Richtigkeit und Konsistenz der Ergebnisse der CADSD Software Tools zu überprüfen, habe ich diese mit den Daten der beiden von Andrea untersuchten Instrumentenformen gefüttert.

Hier die erhaltenen Simulationsergebnisse:

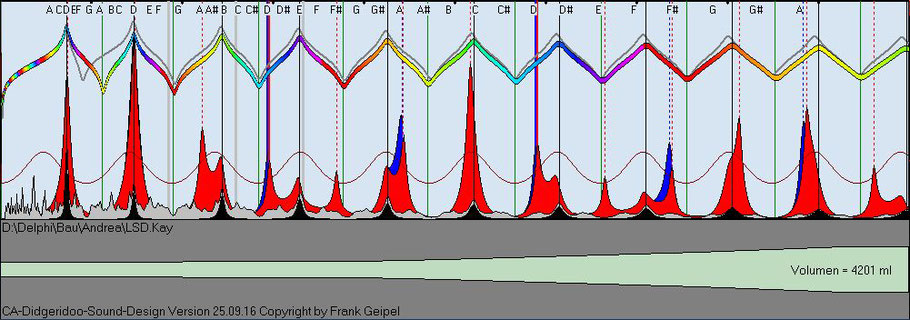
LSD IV Form

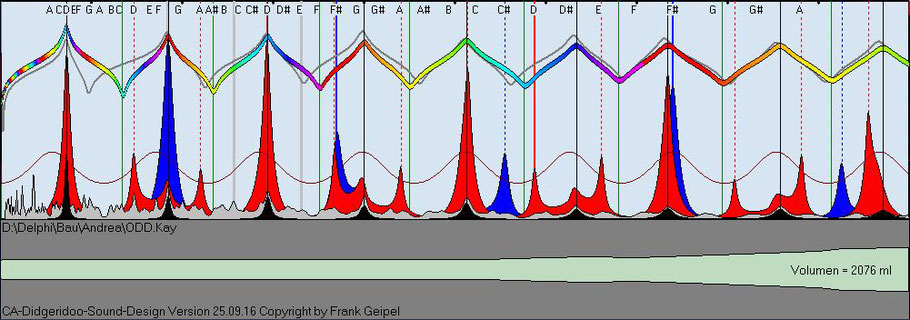
Open Didgeridoo Projekt Form

Die sichtbar unterschiedlichen Spektren bestätigen die von Andrea beschriebenen deutlich verschiedenen Klangqualitäten der beiden Instrumente.

Die nächsten beiden Abbildungen zeigen den Vergleich der mit den verschiedenen Software Tools erhaltenen Simulationsergebnisse:

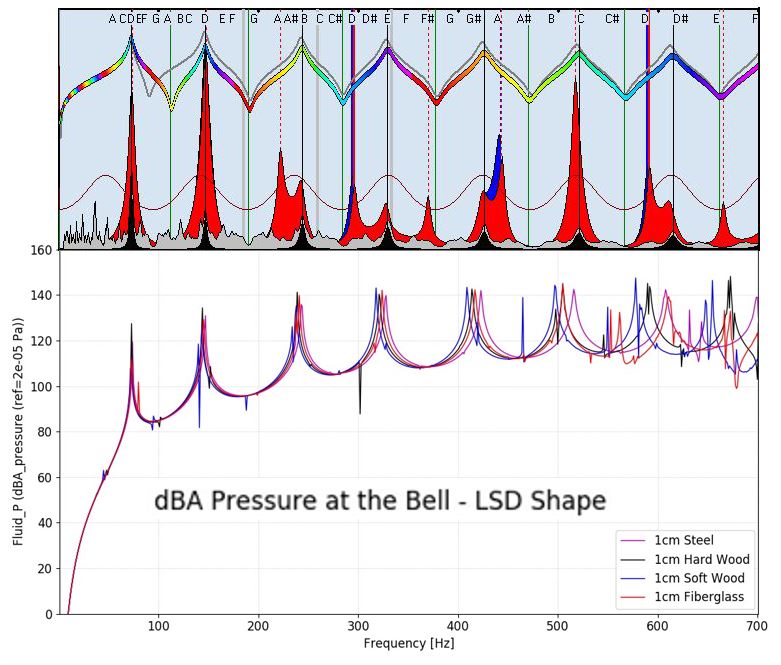
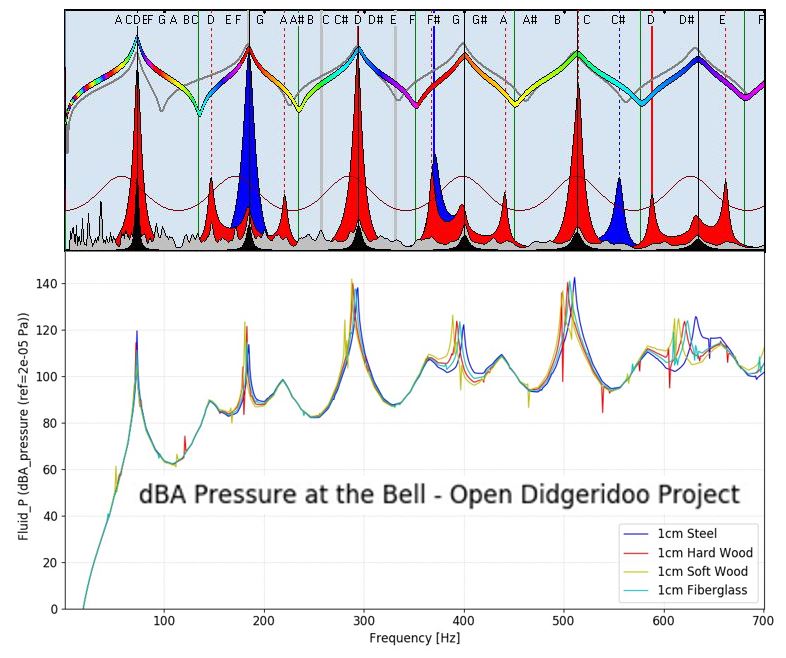
Die plausibel erkennbare Übereinstimmung der Ergebnisse unterstreicht die Qualität der verwendeten Software Tools. Hier zeigt sich auch, dass die in CADSD verwendeten mathematischen Modelle auf die Verwendung von harten steifen Materialien mit hohem E-Modul kalibriert sind, da diese Materialien aus praktischer Erfahrung zu den bevorzugten Baumaterialien gehören.

Zusatzbemerkung:

Wir hatten uns vor einigen Jahren selbst mit dem Stimmen von Xylophonstäben beschäftigt, weil wir damals dachten, dass die Eigenresonanzfrequenzen von festen Schwingungsformen eine wichtige Rolle beim Didgeridoo-Bau spielen. Leider konnten wir diesen Einfluss beim Didgeridoo-Bau weder theoretisch noch experimentell bestätigen. Heute bin ich davon überzeugt, dass das Material eine Rolle spielt, aber eine andere. Es hat sich theoretisch und experimentell gezeigt, dass die erzwungenen Schwingungen, die von der Luftsäule auf das Material übertragen werden, der Luftsäule Energie entziehen und damit die Ausprägung der Obertöne im mittleren bis höheren Bereich selektiv beeinflussen. Dieser Effekt ist schwer zu messen, aber ein geübter Hörer kann ihn durchaus wahrnehmen. Im Allgemeinen gilt: Je härter und steifer das Material ist, desto weniger Energie wird der Luftsäule entzogen. Dadurch wird der Klang analytischer.

Weitere Informationen:

Einfluss von Bau-Material, Wandstärke und Innenoberfläche auf den Klang und die Spielbarkeit   / Frank Geipel 10.08.2024

english ... english ... english ...

The influence of the material on the sound of the didgeridoo /  23.04.2023

Despite the findings already described on this website, there is a recurrent discussion among didgeridoo players and makers, characterized by insufficient basic assumptions and convictions, about the effect of the choice of different materials on the sound of the didgeridoo. In order to first establish a basis for discussion, software-based analyzes and simulations can be carried out for this purpose, exemplified in the following guest article by the well-known Italian engineer and didgeridoo developer Andrea Ferroni.

The article is an excerpt from the book THE DESIGN OF DIDGERIDOO by Andrea Ferroni, 2023, translated and adapted to the website www.didgeridoo-physik.de by Frank Geipel / Ansgar Stein.

COUPLED FLUID DYNAMIC INTERACTION ANALYSIS:
EVALUATION OF MATERIAL INFLUENCE ON SOUND
Andrea Ferroni

The following analysis has been carried out to help enthusiasts and instrument builders understand the importance of each variable that goes into the design of a didgeridoo.

Two shapes were considered for this analysis:

Figure 1: LSD IV shape

The LSD IV shape (Large Spectrum D, IV Variant), is the fourth revision of an instrumental form in D, first realized in 2003,  whose timbre is characterized by the presence of several harmonic and inharmonic components typical of forms resembling irregular cones. The interval between the fundamental and the next higher intrinsic resonance of the air column (1st toot) is exactly one octave.

Figure 2: Open Didgeridoo Shape

The Open Didgeridoo shape, also in D, with an interval between the fundamental and the next higher natural resonance of the air column of a major third above an octave of the fundamental. This second shape represents a compromise between a cylindrical and a conical shape. It gives a clearer timbre because the resonances are further apart than in a conical instrument. At the same time, its timbre is richer than a perfectly cylindrical instrument. Ultimately, this characteristic makes the timbre seem brighter because, due to the lower presence in the range of about 50-700 Hz, the harmonics accentuated by the change in the player’s vocal tract become more prominent at a frequency above 500 Hz, resulting in brilliance.

The following is a summary of the combined and examined variants:

Figure 3: Summary of variants used and combined in this study

Using ACTRAN, the cavity modes of the air column are coupled with the modes and resonances of the instrument body to evaluate possible interactions between air and solid.
In an initial modal analysis, the resonant frequencies of the instrument solid are simulated and the regions where deformations occur are evaluated at each frequency up to 1000 Hz.
Then, similar to other 1D simulation software, the intrinsic resonance frequencies of the cavity (the vibrating air column) and the areas where pressure changes occur due to standing waves are simulated, also in a frequency range up to 1000 Hz.

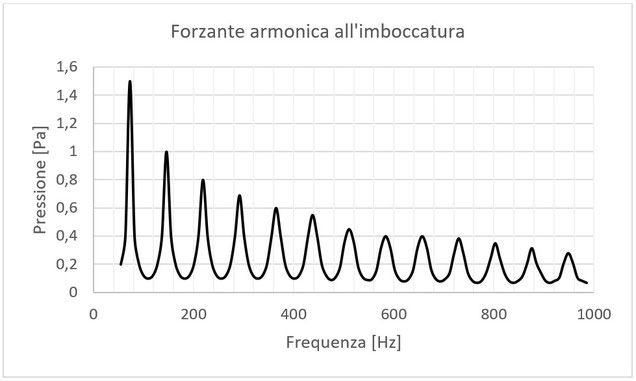
Figure 4: Graphic representation of the pressure excitation in the frequency range from 0-1000 Hz

From here on, the actual specialization of ACTRAN takes effect:
The closed end of the didgeridoo, at the mouthpiece, is subjected to pressure variations that resemble the vibration of a player’s lips - periodic, harmonic pressure variations that yield maxima at the instrument’s perfect fundamental D and all its natural overtones:

Figure 5: Position of the simulated measurement points (yellow);

A series of measurement points (simulated measurement microphones) were placed/simulated 5 cm from the body of the instrument. The first one near the mouthpiece, the second one halfway up, a third one at ¾ of the length of the instrument and a last one in the front of the sound opening, as it would usually be placed in a recording or concert.

It turned out that the simulation results of the various measuring points are extremely similar and differ only in terms of intensity. The greater the distance from the bell end, the lower the intensity by up to -20dB. Based on these results, only the simulated measuring point 5 cm away from the sound opening is considered further. Since the focus of this analysis is the evaluation of the influence of the material on the sound, only the results of the different materials at 1 cm wall thickness are analyzed further.

On my personal PC (Intel®Core™ i7-8700 CPU @ 3.20GHz, 24GB RAM), computing a curve for each simulated measurement microphone described above took about 40 minutes, for each individual material or wall thickness variation. The first four runs examining four materials - steel, hardwood, softwood, fibreglass - are shown below:

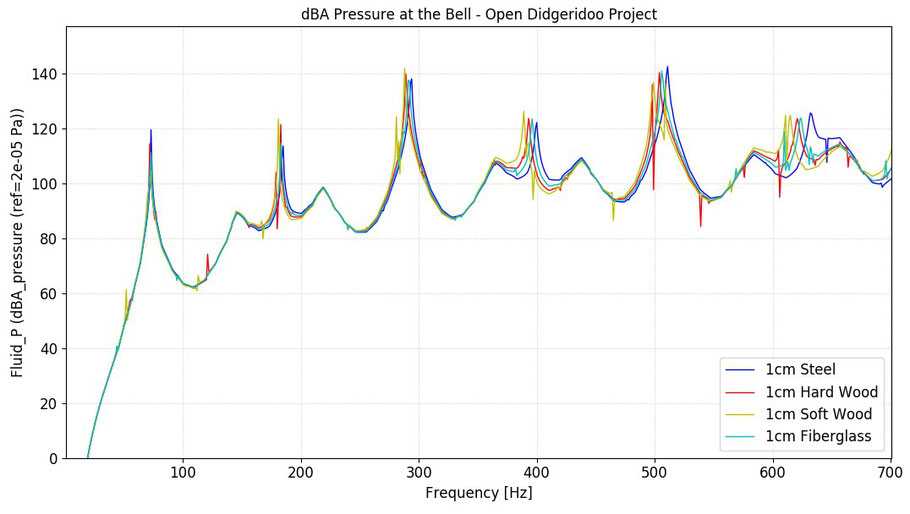
Figure 6: Pressure in dBA at 5 cm from the sound opening. The different colors stand for the 4 materials considered.

The curve profiles are shown here superimposed over the entire frequency range. The largest difference that can be observed is an increasing deviation in the resonant frequencies with increasing frequency.
Between steel and softwood, the difference is 12 Hz at about 500 Hz (499 Hz for a softwood instrument, compared to 511 Hz for an identical steel instrument). Considering that in this frequency range, in the tempered scale (A tuned to 440 Hz), B4 is at 493.88 Hz and C5 is at 523.25 Hz with a semitone interval of 29.37 Hz, the tonal difference due to the material change is less than 25 cents for the 7th harmonic. This difference is reduced to less than 5 Hz between hardwood and softwood and to less than 2 Hz between hardwood and glass fiber, and is thus below the human perception threshold of about 5 cents.

A similar result is obtained with the second form:

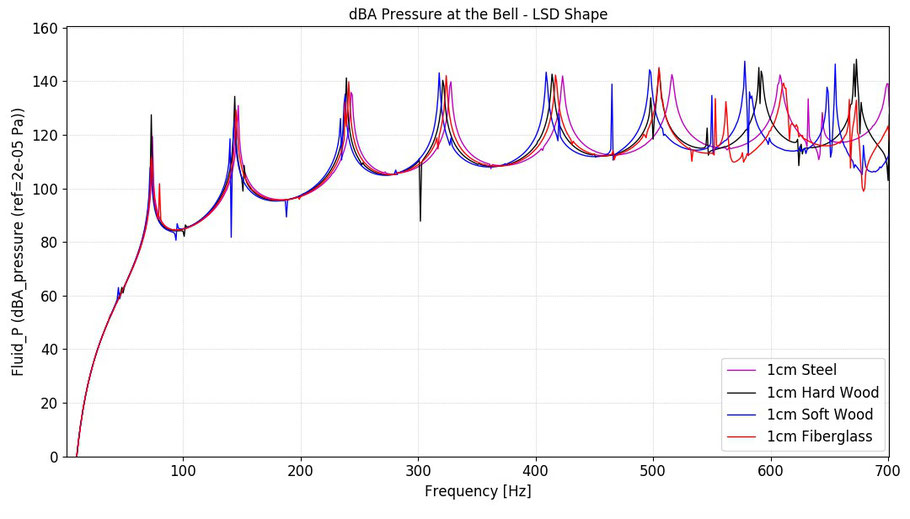
Figure 7: Sound pressure in dBA at 5 cm from the sound opening with the same four materials but with changed shape

Now let’s see the comparison of the two shapes analyzed above:

Figure 8: Overlay of the analyzed shapes

The differences between the Open Didgeridoo (an open source shape) and the LSD IV shape are found in a diameter that is 2 mm larger and more cylindrical on the first 80 cm section of the Open Didgeridoo than on the LSD IV shape. Over a length of 80 to 150 cm, the Open Didgeridoo exhibits a small volume expansion that brings the second resonance to a major third above an octave of the fundamental frequency and then widens toward the ending of the instrument, maintaining a moderate diameter bell. In contrast, the LSD IV shape widens to a length of 80 to 170 cm and then ends in a cylinder about 13 cm long, requiring a much greater overall length to maintain the same fundamental frequency as the previous shape.

The following is a comparison of the simulated spectra of the two instrument shapes with the same material:

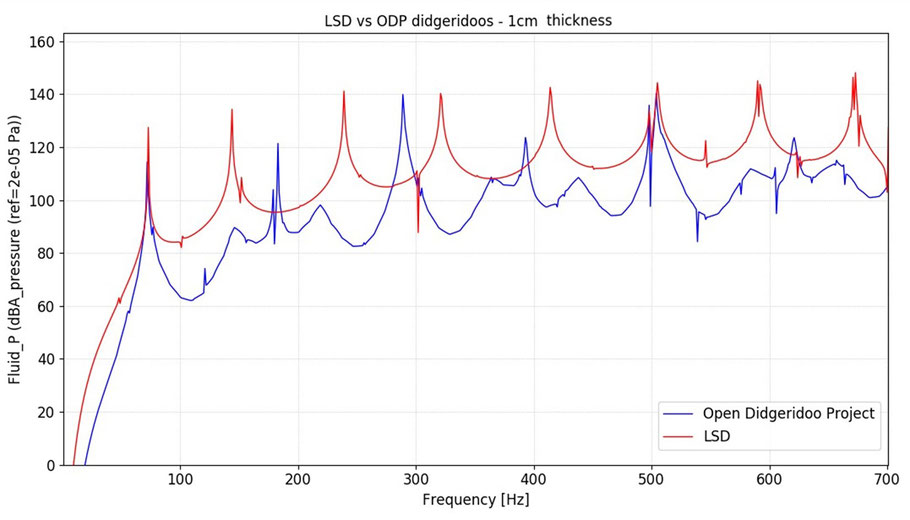
Figure 9: Superposition of the sound intensities of the two shapes using the same materials, with a distance of the simulated measuring microphone of 5 cm from the sound opening

In this case, one can recognize two very different spectra. So different that one might think they are the voices of different people and their pronunciation of different vowels, or even the spectra of different instrument families, because when the two matching fundamental tones are considered in isolation, the different harmonic and inharmonic sound components offer very different timbres.

Another output option of ACTRAN is a plot for the prediction of sound radiation in 360° space. The following figure 10 shows the distribution of sound intensity in dBA inside and outside the instrument in a sphere of 2 m radius:

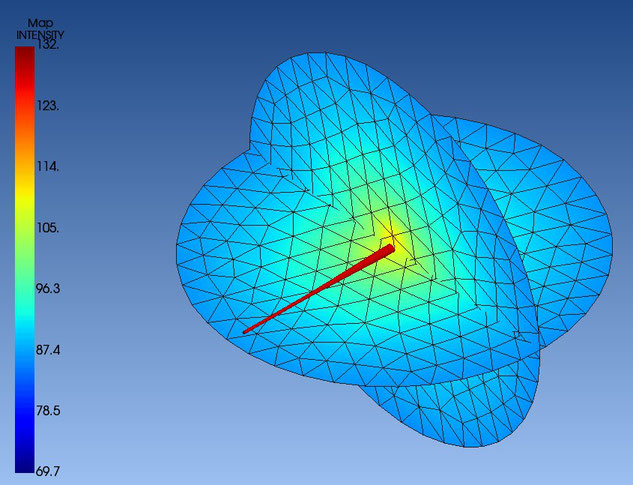
Figure 10: At a fundamental of 73 Hz, you can see in red the interior of the instrument at about 130 dB, down to a minimum of 69.7 dB outside the 2 m spatial sphere

Another output option of ACTRAN is the distribution of the sound pressure, which can be seen in the following figures. While the sound intensity decays with distance from the instrument opening (the sound becomes quieter), the pressure waves show a periodic succession of pressure maxima and pressure minima (assuming the atmospheric pressure is 0) and these decrease with decreasing sound intensity. This is due to the fact that the sound energy density is distributed (diluted) on a 360° spherical surface, which increases with the square of the distance to the sound source.

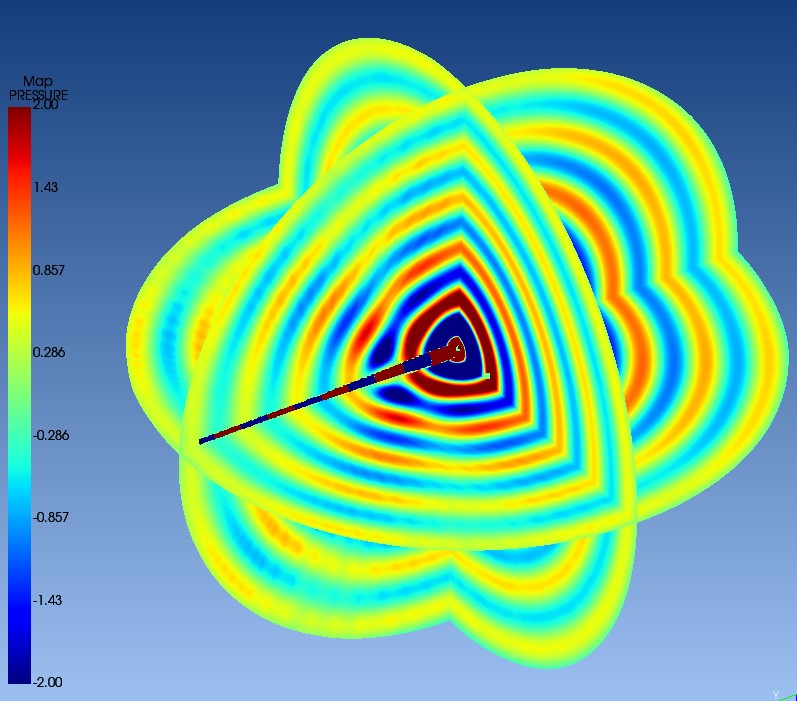
Figure 11: Pressure distribution resulting from blowing the 5th intrinsic resonance frequency (4th toot)

While a coarse finite element grid is sufficient for the simulation and representation of the sound intensity (see the grid in Figure 10), a much denser, finer finite element grid had to be used for the simulation and representation of the sound pressure in order to capture the sinusoidal pattern at an improved resolution. This grid is so dense that it was masked out for better graphical readability.
In the instrument body, the five positively and negatively alternating pressure regions typical of the standing waves of the played 5th intrinsic resonance (4th toot) of a half-closed tube can be clearly seen.

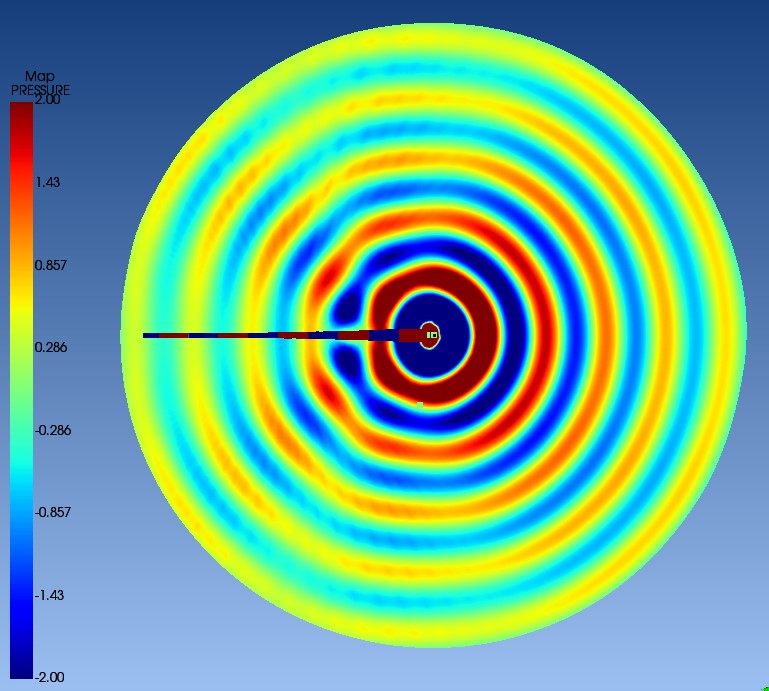
Figure 12: View in the XY plane showing the propagation of the sound pressure waves in space

If the intrinsic oscillations or intrinsic resonances of the vibrating instrument body were to generate a significant sound pressure and thus influence the radiated sound, a series of significant concentric pressure waves would be generated starting from these points. These would collide with the pressure waves coming from the sound aperture and thus create significant interference patterns. However, this is only minimally discernible. All that can be seen is the slight forced transmission (caused by the standing wave of the air column in the instrument) of the standing wave on the instrument body. But this has no significant influence on the radiated sound field and is therefore probably negligible in most cases.

Personal website: www.andreaferroni.it
Didgeridoo outreach site: www.didgeridoo.it 
Didgeridoo research site: www.windproject.it 
YouTube: www.youtube.com/@AndreaFerroni 
Mail: info@andreaferroni.it

Addendum by Frank:

It is always a pleasure to present interesting new contributions on the subject of didgeridoo by enthusiastic people like Andrea Ferroni on this website. Above all, to check the plausibility, correctness and consistency of the results of the CADSD software tools, I fed them with the data of the two instrument shapes examined by Andrea.

Here are the obtained simulation results:

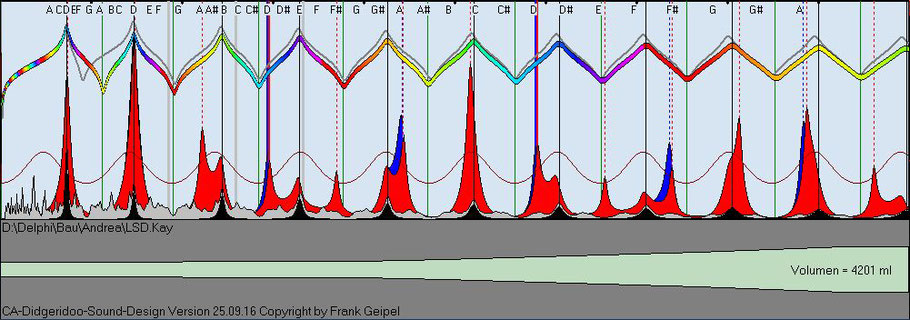
LSD IV Shape

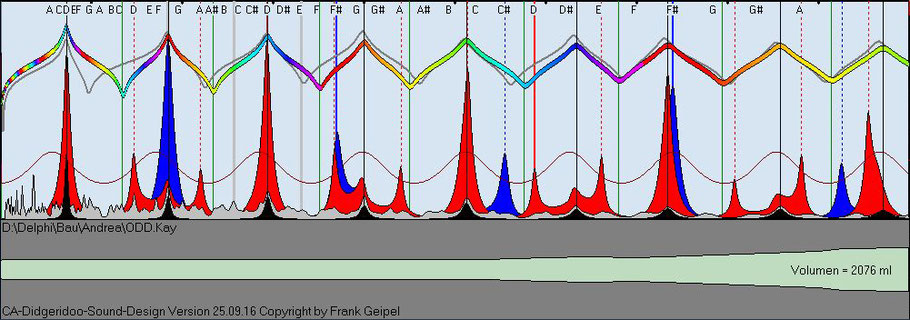
Open Didgeridoo Projekt Shape

The visibly different spectra confirm the clearly different sound qualities of the two instruments described by Andrea.

The next two figures show the comparison of the simulation results obtained with the different software tools:

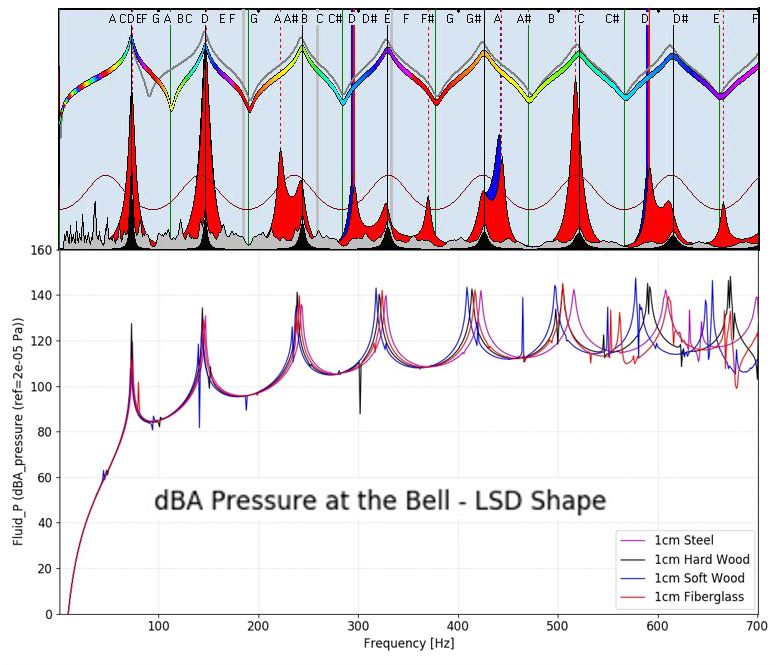
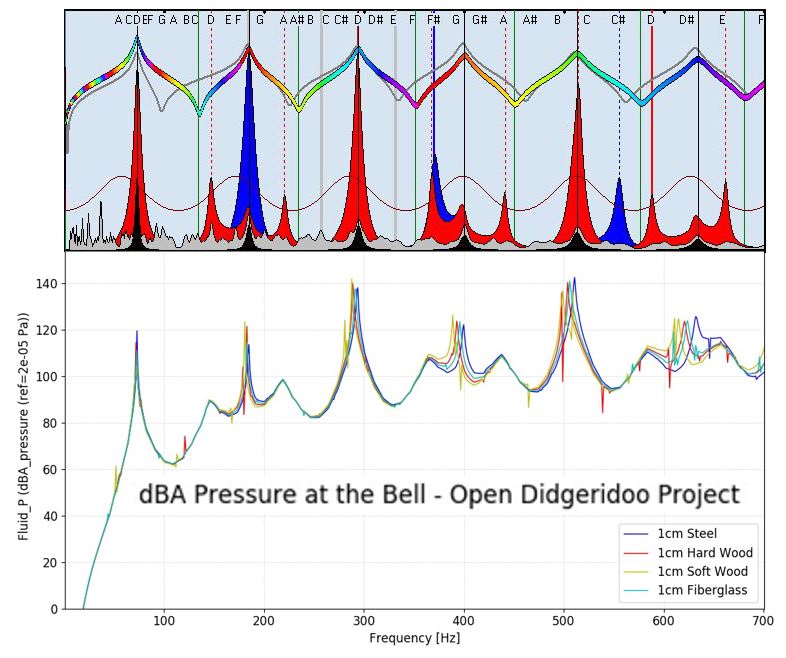
The plausibly recognizable agreement of the results underlines the quality of the software tools used. This also shows that the mathematical models used in CADSD are calibrated to the use of hard, stiff materials with high Young’s modulus, as these materials are among the preferred building materials based on practical experience.

Additional remark:
A few years ago, we had studied the tuning of xylophone bars ourselves because we thought at the time that the natural resonance frequencies of fixed vibration modes play an important role in didgeridoo construction. Unfortunately, we were unable to confirm this influence in didgeridoo construction either theoretically or experimentally. Today I am convinced that the material plays a role, but a different one. It has been shown theoretically and experimentally that the forced vibrations transmitted from the air column to the material extract energy from the air column and thus selectively influence the expression of the overtones in the medium to higher range. This effect is difficult to measure, but an experienced listener can certainly perceive it. In general, the harder and stiffer the material, the less energy is extracted from the air column. This makes the sound more analytical.

Further information:

Influence of building-material, wall-thickness and inner-surface on the sound and playability
/ Frank Geipel 10.08.2024